Ao utilizar as funções de simulação do QucsStudio, a análise de Monte Carlo é uma ferramenta particularmente poderosa. No artigo anterior, explicamos os fundamentos do design de filtro passa-baixa. Desta vez, vamos nos concentrar na função tol na análise de Monte Carlo, explicando em detalhes seu uso e escopo de aplicação.
A razão para enfatizarmos a função tol é que, ao realizar a análise de Monte Carlo, muitos usuários não sabem como definir as variações dos componentes ou realizam simulações incorretas devido à falta de compreensão dos parâmetros. No design de circuitos reais, componentes como resistores e capacitores apresentam variações devido a erros de fabricação e fatores ambientais. Modelar corretamente essas variações é fundamental para melhorar a precisão da simulação.
No entanto, muitos usuários não estão familiarizados com a configuração dos parâmetros da função tol e não conseguem especificar corretamente a amplitude e a distribuição das variações. Como resultado, os resultados da simulação não refletem o comportamento real, levando muitas vezes a conclusões erradas.
Configurando corretamente a função tol, é possível avaliar com mais precisão o desempenho do circuito e simular o impacto de erros de fabricação e variações ambientais. Isso é de grande ajuda para garantir a confiabilidade e o desempenho do circuito durante a fase de projeto.
O que é a simulação de Monte Carlo?
A simulação de Monte Carlo é um método para compreender sistemas ou processos que envolvem incertezas. Ela utiliza várias entradas aleatórias no sistema e repete os cálculos várias vezes. Ao coletar os resultados, é possível analisar a distribuição dos valores e avaliar a frequência e o comportamento dos resultados, permitindo estimar a confiabilidade e o desempenho do sistema.
Por exemplo, se componentes como resistores e capacitores têm uma variação de ±5% no processo de fabricação, o objetivo da análise de Monte Carlo é simular como essa variação afeta o circuito como um todo.
Modelagem da amplitude de variação
Para realizar uma simulação de Monte Carlo, é necessário configurar a variação das variáveis de entrada usadas na simulação. O QucsStudio possui uma função chamada tol que facilita a configuração dessas variações.
Utilizando a função tol, é fácil especificar a amplitude das variações dos dados. Por exemplo, ao definir a amplitude de variação de um resistor específico em torno de seu valor médio, é possível refletir na simulação os erros de fabricação e as variações operacionais. Esta função simula as variações aleatórias das variáveis na análise de Monte Carlo.
Sintaxe da função tol
A função tol do QucsStudio utiliza três argumentos x, v, d para especificar as variações das variáveis e simular flutuações aleatórias.
tol(x, v, d)- x: Valor médio
- v: Intervalo de tolerância (%)
- d: Tipo de distribuição (0 = Distribuição normal, 1 = Distribuição uniforme, padrão é 0)
Por exemplo, para um resistor com uma tolerância de 100Ω ±10%, ele é representado na função tol como segue. O valor médio é especificado como “100” e a amplitude de tolerância de ±10% é definida como “10”.
O que é o tipo de distribuição?
Existem dois tipos de distribuição para a função tol, cada um com características diferentes. A compreensão correta do tipo de distribuição é essencial, pois uma configuração incorreta pode levar a uma simulação fora do intervalo previsto. As diferenças entre a distribuição normal e a distribuição uniforme são:
- Distribuição normal: Os dados são distribuídos simetricamente em torno do valor médio, com uma probabilidade decrescente à medida que se afastam do valor médio. A forma da distribuição é uma curva em forma de sino.
- Distribuição uniforme: Os dados são distribuídos uniformemente em um intervalo especificado, e qualquer valor dentro do intervalo tem a mesma probabilidade de ocorrer. A forma da distribuição é um retângulo.
Os gráficos das distribuições para um valor médio de 100 e uma tolerância de 10% são mostrados abaixo.
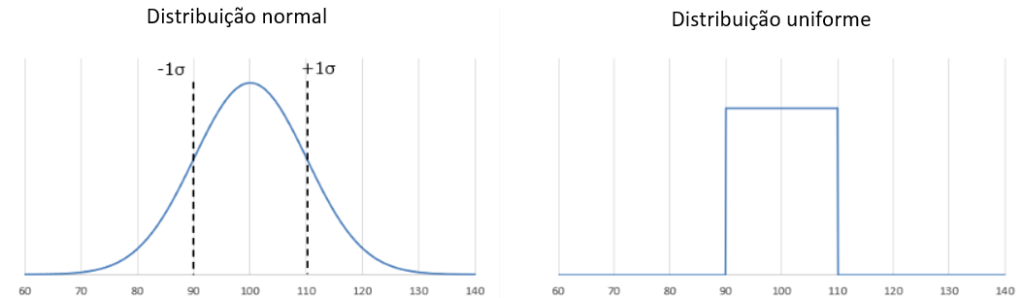
A distribuição normal é centrada em 100, conforme mostrado no gráfico. Se a tolerância (v) for definida como ±10%, isso corresponde a uma distribuição normal com um desvio padrão (σ) de 10Ω. É importante notar que a distribuição pode se estender além do intervalo de 90 a 110Ω, o que significa que as variações não se limitam estritamente a ±10%.
Por outro lado, a distribuição uniforme é simples, cobrindo uma faixa de ±10%, ou seja, de 90 a 110Ω, com dados distribuídos igualmente. No entanto, essa distribuição não é realista para verificar as variações dos componentes reais, pois os componentes reais tendem a ter uma distribuição normal com mais dados concentrados em torno do valor central.
Cuidados ao configurar
As variações dos componentes reais, como resistores e capacitores, seguem uma distribuição normal e não uma distribuição uniforme. No entanto, como mencionado anteriormente, se você definir diretamente a tolerância (v) dos componentes como amplitude de tolerância, a simulação não será precisa. Explicaremos como simular a distribuição real dos componentes em outro artigo.
Conclusão
Ao utilizar a função tol, é possível simular efetivamente variações aleatórias nas variáveis de entrada na análise de Monte Carlo. Compreendendo corretamente as características das distribuições normal e uniforme, e configurando as simulações de forma adequada, é possível avaliar com precisão o desempenho e a confiabilidade do sistema.
コメント