Al utilizar las capacidades de simulación de QucsStudio, el análisis de Monte Carlo es una herramienta especialmente poderosa. En el artículo anterior, explicamos los conceptos básicos del diseño de filtros pasa bajos. Esta vez, nos centraremos en la función tol en el análisis de Monte Carlo, detallando su uso y ámbito de aplicación.
La razón para enfocarse en la función tol es que, al realizar un análisis de Monte Carlo, muchos usuarios no saben cómo configurar las variaciones de los componentes o terminan realizando simulaciones incorrectas debido a una falta de comprensión de los parámetros. En el diseño de circuitos del mundo real, componentes como resistencias y condensadores presentan variaciones debido a errores de fabricación y factores ambientales. Modelar adecuadamente estas variaciones es esencial para mejorar la precisión de la simulación.
Sin embargo, muchos usuarios no están familiarizados con la configuración de los parámetros de la función tol y no pueden especificar correctamente el rango o la distribución de las variaciones. Como resultado, los resultados de la simulación a menudo no reflejan el rendimiento real, lo que lleva a conclusiones incorrectas.
Al configurar correctamente la función tol, se puede evaluar con mayor precisión el rendimiento del circuito y simular los efectos de los errores de fabricación y los cambios ambientales. Esto permite que las consideraciones en la fase de diseño sean más realistas y proporciona una gran ayuda para garantizar la fiabilidad y el rendimiento del circuito.
¿Qué es la simulación de Monte Carlo?
La simulación de Monte Carlo es un método para comprender sistemas o procesos que implican incertidumbre. Esta simulación realiza cálculos repetidamente utilizando varios valores aleatorios como entradas al sistema. Al analizar la distribución resultante, se puede determinar con qué frecuencia ocurren ciertos resultados y evaluar el rendimiento y la fiabilidad del sistema.
Por ejemplo, si los componentes como resistencias o condensadores tienen una variación de ±5% debido a procesos de fabricación, el objetivo del análisis de Monte Carlo es simular cómo estas variaciones afectan al circuito completo.
Modelado del rango de variación
Para realizar una simulación de Monte Carlo, es necesario establecer las variaciones de las variables de entrada utilizadas en la simulación. En QucsStudio, hay una función llamada tol que permite configurar fácilmente estas variaciones.
Al utilizar la función tol, puede especificar fácilmente el rango de variación de los datos. Por ejemplo, al definir cuánto varía un valor específico de resistencia alrededor de su promedio, puede reflejar en la simulación los errores de fabricación y las variaciones del entorno operativo reales. Esta función se utiliza para simular variaciones aleatorias de variables en la simulación de Monte Carlo.
Formato de la función tol
La función tol en QucsStudio especifica las variaciones de las variables y simula fluctuaciones aleatorias utilizando tres argumentos: x, v y d.
tol(x, v, d)- x: Valor medio
- v: Rango de tolerancia (%)
- d: Tipo de distribución (0 = distribución normal, 1 = distribución uniforme, el valor predeterminado es 0)
Por ejemplo, consideremos un resistor con una desviación de 100Ω ±10%. Esto se puede expresar utilizando la función tol de la siguiente manera. El valor medio es el valor central de la variación, por lo que en este caso es «100». El rango de tolerancia indica el grado de variación, por lo que para ±10%, se establece en «10».
¿Qué es el tipo de distribución?
El tipo de distribución de la función tol tiene dos tipos, cada uno con diferentes características. Comprender estos tipos es crucial porque la simulación puede no realizarse dentro del rango esperado si no se entienden correctamente. Las diferencias entre la distribución normal y la distribución uniforme son:
- Distribución Normal (Gaussiana): Los datos se distribuyen simétricamente alrededor del valor medio, y la probabilidad de que ocurra un valor disminuye a medida que se aleja del promedio. La forma de la distribución es una curva de campana.
- Distribución Uniforme: Los datos se distribuyen uniformemente dentro del rango especificado, y cualquier valor dentro del rango tiene la misma probabilidad de ocurrir. La forma de la distribución es rectangular.
Los gráficos de cada distribución, suponiendo un valor medio de 100 y un rango de tolerancia del 10%, son los siguientes:
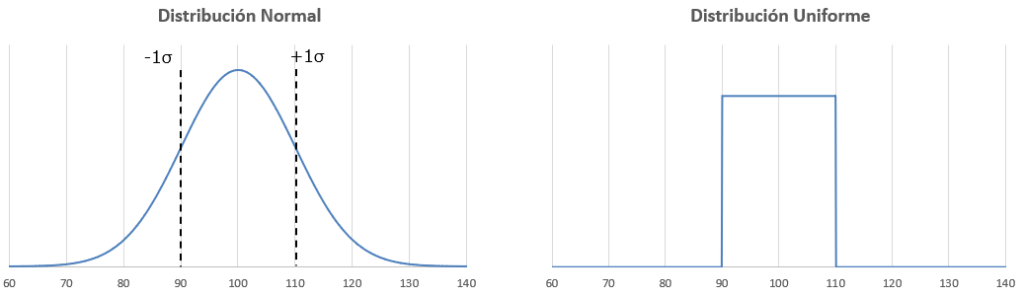
Primero, con la distribución normal, como se muestra en la figura, se convierte en una distribución gaussiana centrada en 100. Configurar el rango de tolerancia (v) a ±10% resulta en una distribución normal con una desviación estándar (σ) de 10Ω. Cabe destacar que también hay distribuciones fuera del rango de 90~110Ω, lo que significa que el rango de variación no es exactamente ±10%.
Para la distribución uniforme, es simple con ±10%, lo que significa que los datos se distribuyen uniformemente de 90 a 110Ω, y no hay datos fuera de este rango. Esto significa que los límites superior e inferior de variación están dentro del rango del 10%. Sin embargo, debido a que la proporción del centro del rango de datos a los límites superior e inferior es igual, no es adecuada para verificar la proporción de variación de los componentes reales. Los componentes electrónicos reales tienen la mayor distribución cerca del centro del rango, con menos variaciones hacia los límites superior e inferior, formando una distribución normal.
Consideraciones importantes para la configuración
En realidad, las variaciones de los componentes como resistencias y condensadores son distribuciones normales, no distribuciones uniformes. Como se mencionó anteriormente, usar directamente la desviación del componente (%) como el rango de tolerancia (v) no permite una simulación precisa. Los métodos para simular la distribución de componentes reales se presentarán en otro artículo.
Conclusión
Al utilizar la función tol, puede simular eficazmente las variaciones aleatorias de las variables de entrada en la simulación de Monte Carlo. Comprender y configurar adecuadamente las características de las distribuciones normal y uniforme permite una evaluación de alta precisión del rendimiento y la fiabilidad del sistema.


コメント