Bei einer Transientenanalyse mit uSimmics (ehemals Qucs) kann man beobachten, dass direkt nach der steigenden Flanke eines Signals die Wellenform unregelmäßig zu schwingen beginnt. Dieses Phänomen wird als Ringing bezeichnet.
Wenn man diese Wellenform zum ersten Mal sieht, denken viele: „Ist da Rauschen überlagert?“ oder „Stimmt etwas mit den Simulationsbedingungen nicht?“. Ringing ist jedoch weder ein zufälliges Phänomen noch ein Simulationsfehler. Es handelt sich um ein grundlegendes physikalisches Phänomen, das sich aus dem natürlichen Verhalten der Schaltung ergibt.
In diesem Artikel verwenden wir uSimmics, um gezielt eine minimale Schaltung zu erzeugen, die ausschließlich Ringing hervorruft, und analysieren anhand der Wellenformen dessen wahre Ursache.
- Gedanken zur Analyse von Ringing in uSimmics
- Ringing ist eines der ersten physikalischen Phänomene im Hochgeschwindigkeitsdesign
- Die Ursache von Ringing: Resonanz zwischen L und C
- Reproduzierbarkeit von Ringing in uSimmics
- Minimale Schaltung zur Beobachtung von Ringing
- Schaltungsparameter (gemeinsame Bedingungen)
- Fall 1: R = 1 Ω
- Fall 2: R = 5 Ω
- Fall 3: R = 10 Ω
- Was man aus dem Vergleich der drei Fälle lernt
- Die minimale Schaltung als Modell einer realen Leiterplatte
- Zusammenfassung
Gedanken zur Analyse von Ringing in uSimmics
Bei der Untersuchung von Ringing in uSimmics ist es wichtig, unnötige Einflussfaktoren zu vermeiden und die Schaltung so einfach wie möglich zu halten.
- Keine Übertragungsleitungen verwenden
- Die Schaltung lokal und kompakt halten
- Eine Konfiguration wählen, die von L und C dominiert wird
Beachtet man diese Punkte, lassen sich die unregelmäßigen Schwingungen direkt nach der steigenden Flanke eindeutig als Ringing durch LC-Resonanz identifizieren.
Ringing ist eines der ersten physikalischen Phänomene im Hochgeschwindigkeitsdesign
Im Design von Hochgeschwindigkeitssignalen ist Ringing oft eines der ersten physikalischen Phänomene, dem Ingenieure begegnen. Schon eine etwas längere Leiterbahn oder der Wechsel zu einem schnelleren IC kann dazu führen, dass zuvor unsichtbare Schwingungen plötzlich auftreten.
Was dabei passiert, ist weder ein Designfehler noch eine Eigenart des Simulators. Lediglich Induktivität (L) und Kapazität (C), die zuvor vernachlässigt werden konnten, werden nun relevant.
Die Ursache von Ringing: Resonanz zwischen L und C
Die grundlegende Ursache von Ringing ist das Vorhandensein von Induktivität (L) und Kapazität (C) in der Schaltung. Leiterbahnen, Vias und Stromschleifen besitzen immer Induktivität, während die Eingangskapazität von ICs und parasitäre Kapazitäten stets vorhanden sind.
Im Moment der steigenden Flanke wird Energie schnell in die Schaltung eingespeist, und es beginnt ein Energieaustausch zwischen L und C. Dieser Austausch ist die Resonanz und zeigt sich als das beobachtete „Zickzack“-Verhalten der Wellenform.
Reproduzierbarkeit von Ringing in uSimmics
Beobachtet man Ringing in uSimmics, fällt auf, dass die Schwingung nahezu immer mit derselben Periode und derselben Form auftritt. Das zeigt, dass Ringing kein zufälliges Rauschen ist, sondern ein durch die Schaltungskonfiguration bestimmtes Phänomen.
Solange L und C konstant bleiben, liefern wiederholte Simulationen nahezu identische Ergebnisse. Diese Reproduzierbarkeit zeigt, dass Ringing ein Phänomen ist, das im Design gezielt behandelt werden kann.
Minimale Schaltung zur Beobachtung von Ringing
Um Ringing zu verstehen, ist es am sinnvollsten, eine minimale Schaltung aufzubauen, in der Ringing der dominierende Effekt ist, ohne andere Effekte wie Reflexion zu vermischen.
Hier bleibt die Topologie der Schaltung unverändert, und nur der Widerstand R wird variiert, um die Wellenformen zu vergleichen.
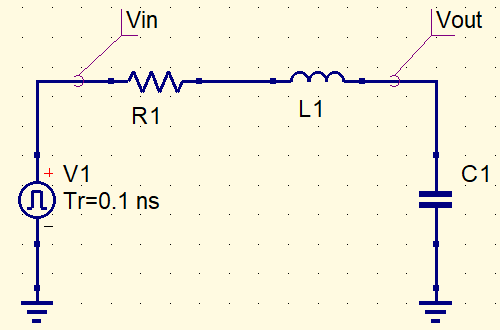
Minimale Schaltung zur Beobachtung von Ringing
VPulse ─ R ─ L ──●── Vout
|
C
|
GND
Der Beobachtungspunkt ist Vout (der obere Anschluss des Kondensators C). An diesem Punkt ist das Ringing direkt nach der steigenden Flanke besonders gut sichtbar.
Schaltungsparameter (gemeinsame Bedingungen)
- VPulse: 0 → 1 V, Tr = 0,1 ns, Tf = 0,1 ns
- L: 10 nH
- C: 10 pF
- R: 1 Ω → 5 Ω → 10 Ω
Bei L = 10 nH und C = 10 pF beträgt die Periode des Ringings etwa 2 ns.
Fall 1: R = 1 Ω
Bei R = 1 Ω ist die Dämpfung gering, sodass das Ringing eine große Amplitude und eine lange Dauer aufweist.
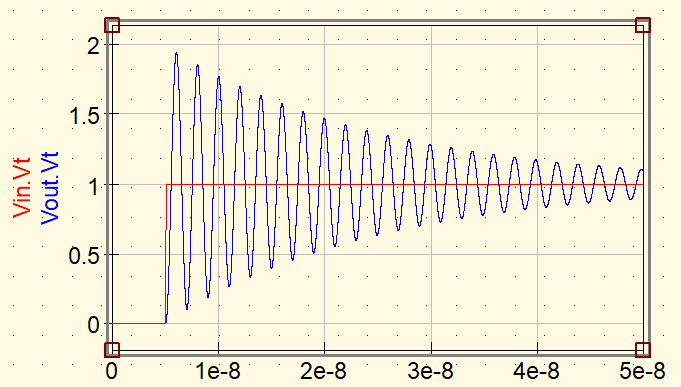
- Große Amplitude
- Lang anhaltende Schwingung
- Periode ≈ 2 ns
Fall 2: R = 5 Ω
Erhöht man R auf 5 Ω, nimmt die Amplitude des Ringings ab, und die Schwingung klingt schneller ab.
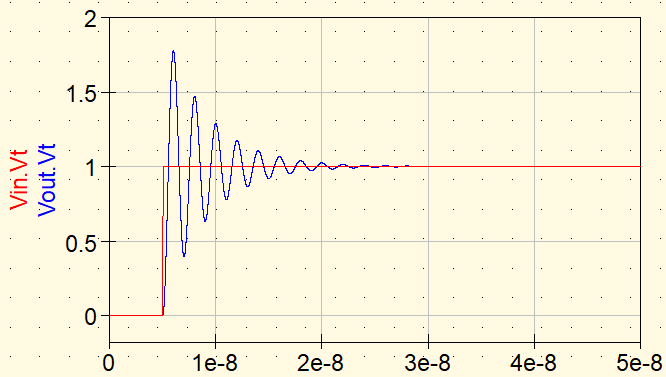
- Periode nahezu unverändert
- Weniger Schwingungszyklen
- Ringing weniger ausgeprägt
Fall 3: R = 10 Ω
Bei R = 10 Ω ist das Ringing stark gedämpft und verschwindet sehr schnell aus der Wellenform.
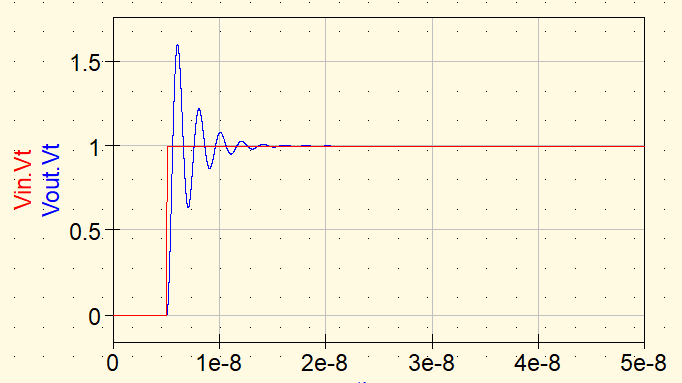
- Periode unverändert
- Sehr kleine Amplitude
- Nicht verschwunden, sondern stark gedämpft
Was man aus dem Vergleich der drei Fälle lernt
- Die Periode des Ringings wird durch L und C bestimmt
- Der Widerstand R verändert nur den Dämpfungsgrad
- Der Widerstand dissipiert Energie und stabilisiert die Schwingung
Die minimale Schaltung als Modell einer realen Leiterplatte
Obwohl diese Schaltung extrem einfach ist, beschreibt sie dasselbe grundlegende Phänomen, das auch auf realen Leiterplatten auftritt.
- Längere Leiterbahnen
- Größere Stromschleifen
- Höhere Eingangskapazität des ICs
All diese Faktoren vergrößern L und C. Die minimale Schaltung in uSimmics macht das Ringing lediglich deutlicher sichtbar und leichter verständlich.
Zusammenfassung
- Ringing wird durch LC-Resonanz verursacht
- Es tritt direkt nach der steigenden Flanke auf
- Die Periode hängt von L und C ab
- Der Widerstand R ist wirksam zur Dämpfung von Ringing
Vergleicht man die Wellenformen für verschiedene R-Werte, wird deutlich, dass Ringing kein „mysteriöses Rauschen“ ist, sondern ein Phänomen, das verstanden und gezielt im Design angepasst werden kann.



Comment