Pourquoi les perles de ferrite fonctionnent : suppression du ringing avec uSimmics

Les perles de ferrite sont très largement utilisées comme mesure de suppression du bruit. On les trouve souvent sur les lignes d’alimentation et les lignes d’E/S, et il n’est pas rare qu’elles soient ajoutées simplement « au cas où ».

Cependant,

• il est difficile d’expliquer clairement pourquoi cela a fonctionné
• on ne comprend pas pourquoi, cette fois-ci, cela n’a pas fonctionné
• la différence avec une inductance reste floue

Utiliser les perles de ferrite dans ces conditions conduit à des décisions de conception fortement dépendantes de l’expérience individuelle.

Dans cet article, nous organisons la question de « pourquoi une perle de ferrite fonctionne » à l’aide d’un modèle de circuit minimal reproductible avec uSimmics (anciennement QucsStudio). La conclusion est claire dès le départ : une perle de ferrite fonctionne non pas parce qu’elle est une inductance.

---

Conclusion de l’article

• Une perle de ferrite n’est pas une inductance idéale
• Son rôle n’est pas de « réfléchir le bruit pour l’arrêter »
• Elle agit en dissipant l’énergie haute fréquence sous forme de pertes (chaleur)
• C’est pourquoi le ringing diminue et le bruit se stabilise

Autrement dit, du point de vue CEM, une perle de ferrite est un composant à pertes dépendantes de la fréquence. Avec cette vision, il devient beaucoup plus facile d’expliquer quand elle fonctionne, quand elle ne fonctionne pas, où la placer et quelles alternatives (R ou RC) peuvent être envisagées.

---

Une idée reçue courante : « ferrite = inductance »

Les perles de ferrite sont souvent décrites comme ayant « une impédance élevée à haute fréquence » ou « une composante inductive ». Ce n’est pas faux, mais cette explication seule laisse subsister une question importante.

Si l’impédance augmente simplement, pourquoi le ringing diminue-t-il ?

Si l’augmentation d’impédance était la seule raison, une réflexion plus forte renforcerait le ringing (augmentation du facteur Q). Pour clarifier ce point, nous examinons d’abord le cas de l’insertion d’une inductance idéale dans uSimmics.

---

Circuit de base commun pour la comparaison dans uSimmics

Le circuit minimal suivant est utilisé comme base commune. Seul l’élément en série est remplacé afin de comparer quatre cas. Le point d’observation est Vout (borne supérieure de Cload).

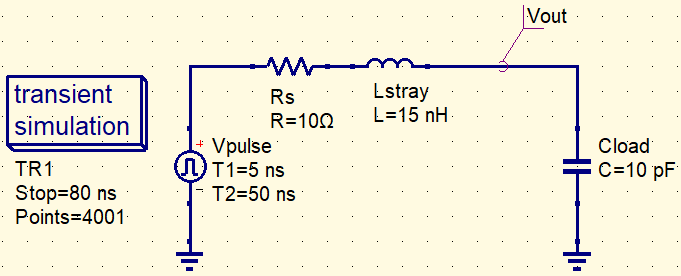
Paramètres recommandés (exemple)

Les valeurs suivantes sont données à titre d’exemple afin de comparer clairement le ringing et l’effet de la perle de ferrite dans uSimmics. Ajustez les temps de montée et les valeurs des composants selon votre circuit réel.

Élément	Valeur	Objectif
VPulse	0 → 1 V	Observer clairement la réponse à l’échelon
Tr / Tf	1 ns	Comparaison stable des formes d’onde
Largeur d’impulsion	50 ns	Observer le comportement après le front
Rs	10 Ω	Modèle de résistance de sortie du driver
Lstray	15 nH	Inductance parasite (pistes/boîtier)
Cload	10 pF	Charge + capacité parasite

Réglage Transient (exemple)

• Stop time : 80 ns
• Max step : 20 ps (réduire si le ringing est insuffisant)

Note : ces valeurs sont choisies à des fins pédagogiques. Pour une carte réelle, remplacez L/C/R par des valeurs représentatives.

---

Comparaison des formes d’onde : quatre cas dans les mêmes conditions

Quatre formes d’onde sont présentées ci-dessous. Veillez à conserver les mêmes échelles X/Y pour les quatre graphiques afin de faciliter la comparaison.

Forme d’onde ① : Sans contre-mesure

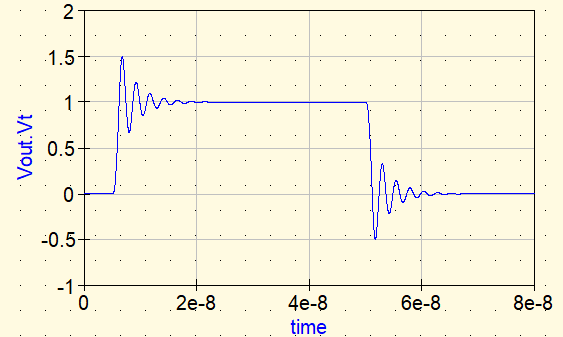
Sans contre-mesure, Vout présente un dépassement puis un ringing persistant. Ce phénomène est dû à la résonance formée par Lstray et Cload. Plus les pertes sont faibles, plus l’oscillation dure longtemps.

---

Forme d’onde ② : Inductance idéale

Nous insérons ensuite une inductance idéale en série.

• Lideal : 100 nH (exemple)

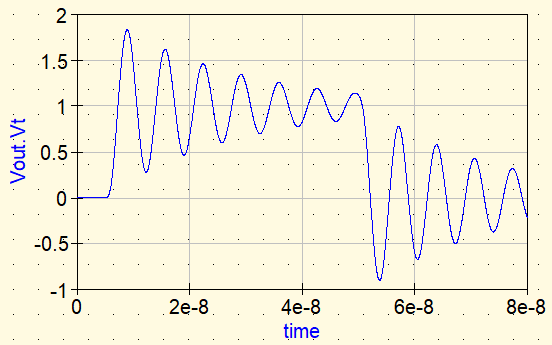
Il est tentant de penser qu’une impédance plus élevée à haute fréquence suffira à arrêter le bruit. Cependant, une inductance idéale ne dissipe aucune énergie. L’énergie résonante reste dans le circuit et le ringing ne se stabilise pas rapidement.

Point clé : ce n’est pas l’augmentation d’impédance qui supprime le ringing, mais la présence de pertes.

---

Forme d’onde ③ : Résistance idéale

Nous insérons ensuite une résistance idéale en série.

• Rideal : 10 Ω (exemple)

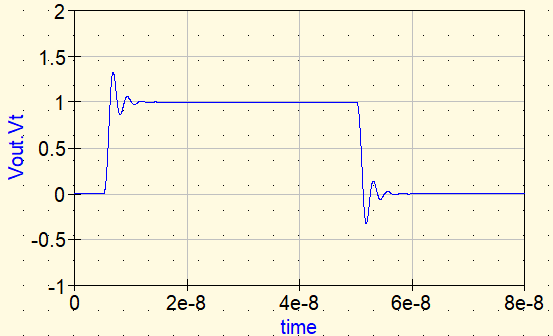
Avec la résistance, le ringing s’atténue visiblement. La raison est simple : l’énergie de l’oscillation est dissipée sous forme de chaleur.

Autrement dit, ce qui arrête réellement le ringing n’est pas l’impédance, mais la perte (R).

---

Forme d’onde ④ : Perle de ferrite

Enfin, nous réalisons une simulation avec une perle de ferrite réelle. Elle est insérée en série sous forme de paramètres S (2 ports).

• Perle utilisée : BLM03AG601SN1 (Murata)
• Paramètres S (.s2p) : disponibles sur le site de Murata

La perle de ferrite ayant une réponse dépendante de la fréquence, l’utilisation de paramètres S permet d’observer un comportement beaucoup plus réaliste dans le domaine temporel.

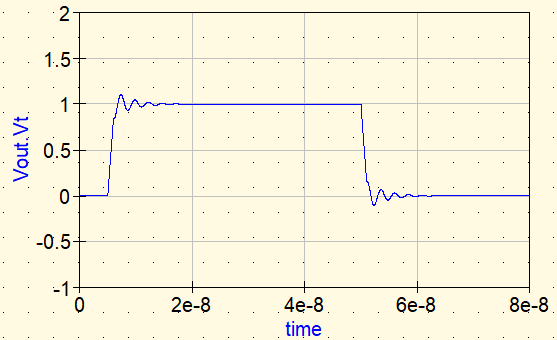
En insérant la perle de ferrite via des paramètres S, le ringing est amorti de manière similaire au cas de la résistance idéale. La différence essentielle réside dans la dépendance fréquentielle.

Alors qu’une résistance introduit des pertes dès le continu, la perle de ferrite augmente les pertes principalement dans la bande de haute fréquence visée. Elle dissipe ainsi l’énergie des composantes haute fréquence du front tout en limitant l’impact sur le continu et les basses fréquences.

---

Ce que montre la comparaison des quatre formes d’onde

• Sans contre-mesure : la résonance apparaît directement
• Inductance idéale : difficile à amortir (pas de pertes)
• Résistance idéale : amortissement efficace (pertes présentes)
• Perle de ferrite : amortissement efficace (pertes à haute fréquence)

Ainsi, une perle de ferrite fonctionne non pas parce qu’elle est une inductance, mais parce qu’elle introduit des pertes, de manière sélective en fréquence.

---

Pourquoi ne pas utiliser simplement une résistance ?

Il est naturel de se demander : « pourquoi ne pas simplement ajouter une résistance ? ». En effet, une résistance permet de supprimer le ringing.

Cependant, une résistance présente plusieurs inconvénients :

• Chute de tension même en continu
• Dissipation de puissance accrue
• Impact plus important sur le signal ou la qualité de l’alimentation

À l’inverse, une perle de ferrite a peu d’effet en continu et à basse fréquence, tout en étant efficace là où cela est nécessaire. On peut donc la considérer comme une « résistance qui n’agit que là où il faut ».

---

Cas typiques où la perle fonctionne / ne fonctionne pas

Cas où elle fonctionne bien

• Ringing haute fréquence sur les lignes d’alimentation
• Bruit dû aux fronts rapides des signaux numériques
• Lorsque les émissions rayonnées sont dominées par des composantes haute fréquence

Cas où elle ne fonctionne pas ou peut aggraver la situation

• Le bruit dominant est de basse fréquence et hors de la bande de pertes
• Une nouvelle résonance est créée après la perle
• Le chemin de retour (GND) est long et l’énergie n’est pas dissipée comme prévu

---

L’emplacement est essentiel : où la placer

Une perle de ferrite n’est pas un « mur ». C’est avant tout une sortie permettant d’évacuer l’énergie.

Son efficacité est maximale lorsqu’elle est placée :

• Près de la source de bruit
• Juste avant que l’énergie haute fréquence ne se propage
• À un endroit où le chemin de retour (GND) est court

Tenir compte de ces points permet de maximiser l’effet de la perle de ferrite.

---

Résumé

Une perle de ferrite fonctionne non pas parce qu’elle est une inductance, mais parce qu’elle dissipe l’énergie haute fréquence sous forme de pertes. C’est pourquoi une inductance idéale n’arrête pas le ringing, tandis qu’une résistance ou une perle de ferrite permet une stabilisation plus rapide de la forme d’onde.

Cela dit, une perle de ferrite n’est pas universelle. Si sa caractéristique de pertes ne correspond pas à la fréquence du ringing, la forme d’onde peut être très proche du cas sans contre-mesure. L’emplacement et le chemin de retour jouent également un rôle déterminant.

En comparant les circuits dans uSimmics, on peut constater sur les formes d’onde que ce n’est pas simplement une « impédance élevée » qui est efficace, mais bien où et à quelle fréquence l’énergie est amortie. Cette visualisation permet de considérer la perle de ferrite non comme un composant « ajouté par habitude », mais comme un outil de conception utilisé de manière raisonnée.