Lors de l’utilisation des fonctionnalités de simulation de QucsStudio, l’analyse de Monte-Carlo est un outil particulièrement puissant. Dans l’article précédent, nous avons expliqué les bases de la conception de filtres passe-bas. Cette fois-ci, nous nous concentrerons sur la fonction tol dans l’analyse de Monte-Carlo, et expliquerons en détail son utilisation et son champ d’application.
La raison pour laquelle nous mettons l’accent sur la fonction tol est que, lors de l’exécution de l’analyse de Monte-Carlo, de nombreux utilisateurs ne savent pas comment définir les variations des composants, ou effectuent des simulations incorrectes en raison d’une mauvaise compréhension des paramètres. Dans la conception de circuits réels, des composants tels que les résistances et les condensateurs présentent des variations dues aux erreurs de fabrication et aux facteurs environnementaux. Modéliser correctement ces variations est essentiel pour améliorer la précision de la simulation.
Cependant, de nombreux utilisateurs ne sont pas familiers avec les paramètres de la fonction tol et ne parviennent pas à spécifier correctement l’étendue et la distribution des variations. En conséquence, les résultats de simulation ne reflètent pas le comportement réel, ce qui peut conduire à des conclusions erronées.
En configurant correctement la fonction tol, il est possible d’évaluer plus précisément les performances du circuit et de simuler l’impact des erreurs de fabrication et des variations environnementales. Cela aide grandement à garantir la fiabilité et les performances du circuit lors de la phase de conception.
Qu’est-ce que la simulation de Monte-Carlo ?
La simulation de Monte-Carlo est une méthode pour comprendre des systèmes ou des processus incertains. Elle consiste à utiliser de nombreuses valeurs aléatoires comme entrées du système et à répéter les calculs plusieurs fois. En collectant les résultats, on peut examiner la distribution des valeurs et évaluer la fréquence et le comportement des résultats, ce qui permet d’estimer la fiabilité et les performances du système.
Par exemple, si des composants tels que des résistances et des condensateurs ont une variation de ±5% dans le processus de fabrication, l’objectif de l’analyse de Monte-Carlo est de simuler comment cette variation affecte l’ensemble du circuit.
Modélisation des plages de variation
Pour réaliser une simulation de Monte-Carlo, il est nécessaire de configurer la variation des variables d’entrée utilisées dans la simulation. QucsStudio dispose d’une fonction appelée tol qui facilite la configuration de ces variations.
En utilisant la fonction tol, il est facile de spécifier la plage de variations des données. Par exemple, en définissant l’étendue des variations d’une résistance spécifique autour de sa valeur moyenne, il est possible de refléter les erreurs de fabrication et les variations de fonctionnement dans la simulation. Cette fonction simule les variations aléatoires des variables dans l’analyse de Monte-Carlo.
Syntaxe de la fonction tol
La fonction tol de QucsStudio utilise trois arguments x, v, d pour spécifier les variations des variables et simuler les fluctuations aléatoires.
tol(x, v, d)- x : Valeur moyenne
- v : Plage de tolérance (%)
- d : Type de distribution (0 = Distribution normale, 1 = Distribution uniforme, par défaut 0)
Par exemple, pour une résistance avec une tolérance de 100Ω ±10%, elle est représentée dans la fonction tol comme suit. La valeur moyenne est spécifiée comme « 100 » et la plage de tolérance de ±10% est définie comme « 10 ».
Qu’est-ce que le type de distribution ?
Il existe deux types de distributions pour la fonction tol, chacune ayant des caractéristiques différentes. La compréhension correcte du type de distribution est essentielle, car une mauvaise configuration peut conduire à une simulation en dehors de la plage prévue. Les différences entre la distribution normale et la distribution uniforme sont :
- Distribution normale : Les données sont distribuées de manière symétrique autour de la valeur moyenne, avec une probabilité de moins en moins élevée à mesure qu’elles s’éloignent de la moyenne. La forme de la distribution est une courbe en cloche.
- Distribution uniforme : Les données sont réparties de manière égale dans une plage spécifiée, chaque valeur de la plage ayant une probabilité égale d’apparition. La forme de la distribution est rectangulaire.
Les graphiques des distributions pour une valeur moyenne de 100 et une plage de tolérance de 10 % sont illustrés ci-dessous.
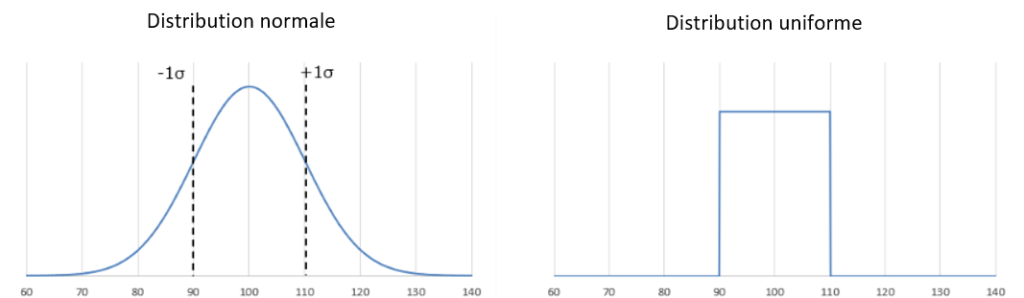
La distribution normale est centrée autour de 100, comme le montre le graphique. Si la tolérance (v) est définie à ±10 %, cela correspond à une distribution normale avec un écart-type (σ) de 10Ω. Il est important de noter que la distribution peut s’étendre en dehors de la plage de 90 à 110Ω, ce qui signifie que les variations ne se limitent pas strictement à ±10 %.
En revanche, la distribution uniforme est simple, couvrant une plage de ±10 %, c’est-à-dire de 90 à 110Ω, avec des données réparties de manière égale. Cependant, cette distribution n’est pas réaliste pour la vérification des variations des composants réels, car les composants réels ont tendance à avoir une distribution normale avec plus de données concentrées autour de la valeur centrale.
Précautions lors de la configuration
Les variations des composants réels, tels que les résistances et les condensateurs, suivent une distribution normale plutôt qu’une distribution uniforme. Cependant, comme mentionné précédemment, si vous définissez directement la tolérance (v) des composants comme plage de tolérance, la simulation ne sera pas précise. Nous expliquerons comment simuler la distribution réelle des composants dans un autre article.
Conclusion
En utilisant la fonction tol, vous pouvez simuler efficacement les variations aléatoires des variables d’entrée dans l’analyse de Monte-Carlo. En comprenant correctement les caractéristiques des distributions normale et uniforme, et en configurant les simulations en conséquence, il est possible d’évaluer avec précision les performances et la fiabilité du système.
📌 Voir l’ordre de lecture recommandé (Roadmap)
➡️ À lire ensuite : Modélisation réaliste des tolérances (écart-type / σ)


Comment