Ferritperlen werden sehr häufig als Maßnahme zur Rauschunterdrückung eingesetzt. Man findet sie in Versorgungsleitungen und E/A-Leitungen, und nicht selten werden sie einfach „vorsorglich“ bestückt.
Allerdings gilt oft:
- Man kann nicht klar erklären, warum es funktioniert hat
- Man versteht nicht, warum es diesmal nicht funktioniert hat
- Der Unterschied zu einer Induktivität bleibt unklar
Wer Ferritperlen auf diese Weise verwendet, läuft Gefahr, dass Designentscheidungen stark von persönlicher Erfahrung abhängen.
In diesem Artikel ordnen wir die Frage „Warum wirken Ferritperlen?“ anhand eines minimalen Schaltungsmodells, das mit uSimmics (ehemals QucsStudio) reproduziert werden kann. Die zentrale Aussage vorweg: Ferritperlen wirken nicht deshalb, weil sie Induktivitäten sind.
- Fazit des Artikels
- Ein häufiger Irrtum: „Ferrit = Induktivität“
- Gemeinsame Basisschaltung für den Vergleich in uSimmics
- Wellenformvergleich: Vier Varianten unter gleichen Bedingungen
- Was der Vergleich der vier Wellenformen zeigt
- Warum nicht einfach einen Widerstand verwenden?
- Typische Fälle: Wirksam / Nicht wirksam
- Die Platzierung ist entscheidend
- Zusammenfassung
Fazit des Artikels
- Eine Ferritperle ist keine ideale Induktivität
- Ihr Wesen ist nicht, „Störungen zu reflektieren und zu stoppen“
- Sie wirkt, indem sie hochfrequente Energie als Verlust (Wärme) abbaut
- Dadurch wird das Ringing gedämpft und das Signal stabilisiert
Mit anderen Worten: Aus EMV-Sicht ist eine Ferritperle ein frequenzabhängiges Verlustelement. Mit dieser Sichtweise lassen sich Wirkung, Nicht-Wirkung, Platzierung und auch Alternativen (R oder RC) deutlich besser erklären.
Ein häufiger Irrtum: „Ferrit = Induktivität“
Ferritperlen werden oft mit Aussagen wie „hohe Impedanz bei hoher Frequenz“ oder „induktive Komponente“ beschrieben. Das ist nicht falsch, greift jedoch zu kurz.
Wenn die Impedanz einfach nur steigt – warum nimmt dann das Ringing ab?
Wäre eine höhere Impedanz allein ausschlaggebend, würden stärkere Reflexionen das Ringing eher verstärken (höherer Q-Faktor). Um das zu klären, betrachten wir zunächst den Fall einer idealen Induktivität in uSimmics.
Gemeinsame Basisschaltung für den Vergleich in uSimmics
Die folgende minimale Schaltung dient als gemeinsame Basis. Es wird lediglich das serielle Element ausgetauscht, um vier Varianten zu vergleichen. Der Beobachtungspunkt ist Vout (oberer Anschluss von Cload).
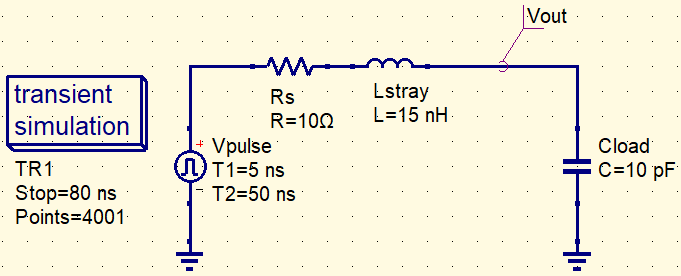
Empfohlene Parameter (Beispiel)
Die folgenden Werte sind lediglich ein Beispiel, um Ringing und den Effekt der Ferritperle in uSimmics anschaulich zu vergleichen. Passen Sie Anstiegszeit und Bauteilwerte an Ihre reale Schaltung an.
| Parameter | Wert | Zweck |
|---|---|---|
| VPulse | 0 → 1 V | Klare Beobachtung der Sprungantwort |
| Tr / Tf | 1 ns | Vergleichbare Anstiegs-/Abfallzeit |
| Pulsbreite | 50 ns | Ausreichende Beobachtung nach dem Flankenwechsel |
| Rs | 10 Ω | Modell des Treiber-Ausgangswiderstands |
| Lstray | 15 nH | Parasitäre Induktivität (Leiterbahn/Gehäuse) |
| Cload | 10 pF | Last- und parasitäre Kapazität |
Transient-Einstellungen (Beispiel)
- Stop time: 80 ns
- Max step: 20 ps (weiter verkleinern, falls Ringing nicht sichtbar wird)
Hinweis: Diese Werte dienen der Veranschaulichung. Für reale Leiterplatten sollten L/C/R entsprechend angepasst werden.
Wellenformvergleich: Vier Varianten unter gleichen Bedingungen
Im Folgenden werden vier Wellenformen verglichen. Achten Sie darauf, für alle die gleiche X-/Y-Skalierung zu verwenden, um Unterschiede klar zu erkennen.
Wellenform ①: Ohne Gegenmaßnahme
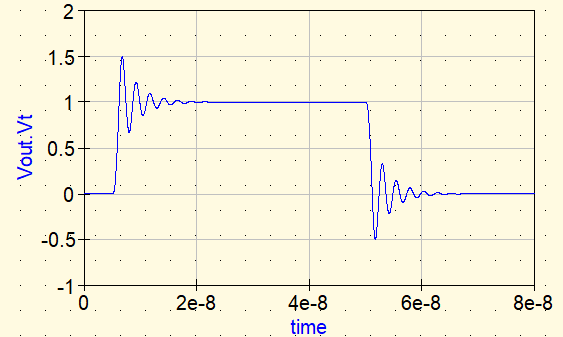
Ohne Gegenmaßnahme zeigt Vout nach der steigenden Flanke ein Überschwingen und anschließendes Ringing. Ursache ist die Resonanz aus Lstray und Cload. Je geringer die Verluste, desto länger hält die Schwingung an.
Wellenform ②: Ideale Induktivität
Als Nächstes wird eine ideale Induktivität in Serie eingefügt.
- Lideal: 100 nH (Beispiel)
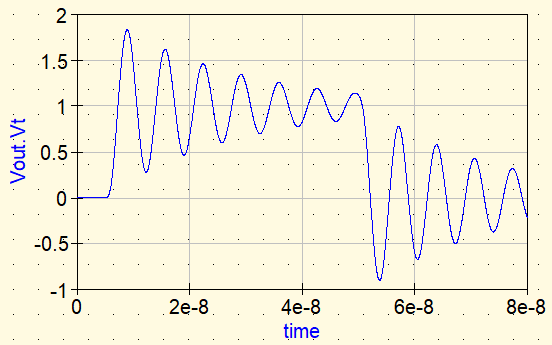
Es klingt plausibel anzunehmen, dass eine höhere Impedanz bei hohen Frequenzen das Problem löst. Eine ideale Induktivität besitzt jedoch keine Verluste. Die Resonanzenergie bleibt im System, und das Ringing klingt nur langsam ab.
Wichtiger Punkt: Nicht die hohe Impedanz stoppt das Ringing, sondern vorhandene Verluste.
Wellenform ③: Idealer Widerstand
Anschließend wird ein idealer Widerstand in Serie eingefügt.
- Rideal: 10 Ω (Beispiel)
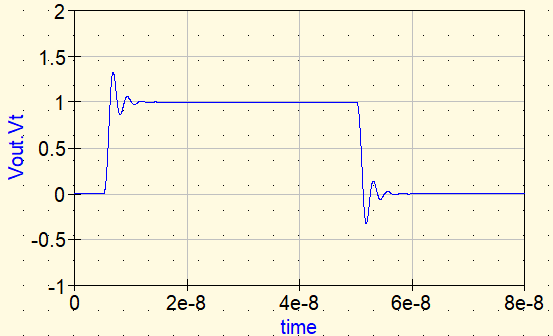
Mit dem Widerstand nimmt das Ringing deutlich ab. Der Grund ist einfach: Die Schwingungsenergie wird als Wärme im Widerstand umgesetzt.
Mit anderen Worten: Was das Ringing wirklich beendet, ist nicht die Impedanz, sondern der Verlust (R).
Wellenform ④: Ferritperle
Zum Schluss simulieren wir eine reale Ferritperle. Sie wird als S-Parameter-Modell (2-Port) in Serie eingefügt.
- Verwendete Ferritperle: BLM03AG601SN1 (Murata)
- S-Parameter (.s2p): verfügbar auf der Murata-Webseite
Da Ferritperlen ein frequenzabhängiges Verhalten zeigen, ermöglicht die Verwendung von S-Parametern eine realistischere Betrachtung im Zeitbereich.
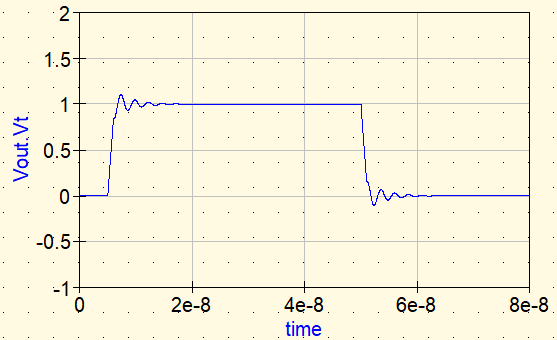
Wird die Ferritperle über S-Parameter eingefügt, zeigt sich eine ähnliche Dämpfung wie beim idealen Widerstand. Der entscheidende Unterschied liegt in der Frequenzabhängigkeit.
Während ein Widerstand Verluste bereits bei Gleichspannung verursacht, erhöhen Ferritperlen die Verluste hauptsächlich im gewünschten Hochfrequenzbereich. So wird die Energie der hochfrequenten Signalanteile dissipiert, ohne DC- und Niederfrequenzanteile stark zu beeinflussen.
Was der Vergleich der vier Wellenformen zeigt
- Ohne Maßnahme: Die Resonanz ist direkt sichtbar
- Ideale Induktivität: Schwer zu dämpfen (keine Verluste)
- Idealer Widerstand: Effektive Dämpfung (Verluste vorhanden)
- Ferritperle: Effektive Dämpfung (Verluste bei hohen Frequenzen)
Daraus folgt: Eine Ferritperle wirkt nicht, weil sie eine Induktivität ist, sondern weil sie Verluste einbringt – und das frequenzselektiv.
Warum nicht einfach einen Widerstand verwenden?
Die Frage liegt nahe: „Warum nicht einfach einen Widerstand einsetzen?“ Tatsächlich kann ein Widerstand das Ringing unterdrücken.
Ein Widerstand bringt jedoch Nachteile mit sich:
- Spannungsabfall auch bei DC
- Erhöhte Verlustleistung
- Stärkerer Einfluss auf Signal- oder Versorgungsqualität
Ferritperlen hingegen haben kaum Einfluss bei DC und niedrigen Frequenzen und wirken gezielt dort, wo es nötig ist. Man kann sie daher als „Widerstand, der nur dort wirkt, wo er gebraucht wird“ betrachten.
Typische Fälle: Wirksam / Nicht wirksam
Typische wirksame Anwendungen
- Hochfrequentes Ringing auf Versorgungsleitungen
- Störungen durch schnelle Flanken digitaler Signale
- Abgestrahlte Störungen mit dominanten Hochfrequenzanteilen
Fälle, in denen sie nicht wirkt oder schadet
- Die dominante Störung ist niederfrequent und liegt außerhalb des Verlustbereichs
- Hinter der Ferritperle entsteht eine neue Resonanz
- Der Rückstrompfad (GND) ist lang, sodass Energie nicht wie erwartet dissipiert wird
Die Platzierung ist entscheidend
Eine Ferritperle ist keine „Wand“. Vielmehr ist sie ein Abfluss für Energie.
Ihre Wirkung ist daher am größten, wenn sie platziert wird:
- Nahe an der Störquelle
- Unmittelbar bevor hochfrequente Energie weitergeleitet wird
- An einer Stelle mit kurzem Rückstrompfad (GND)
Eine durchdachte Platzierung maximiert die Wirksamkeit der Ferritperle.
Zusammenfassung
Ferritperlen wirken nicht deshalb, weil sie Induktivitäten sind, sondern weil sie hochfrequente Energie als Verlust abbauen. Daher kann eine ideale Induktivität das Ringing nicht stoppen, während Widerstände und Ferritperlen – als verlustbehaftete Elemente – eine schnellere Stabilisierung ermöglichen.
Gleichzeitig sind Ferritperlen kein Allheilmittel. Stimmen ihre Verlustcharakteristik und die Ringing-Frequenz nicht überein, kann die Wellenform nahezu identisch zum Fall ohne Gegenmaßnahme sein. Auch Platzierung und Rückstrompfad spielen eine entscheidende Rolle.
Der Vergleich von Schaltungen in uSimmics zeigt deutlich: Nicht eine „hohe Impedanz“ ist ausschlaggebend, sondern wo und bei welcher Frequenz Energie gedämpft wird. Diese Visualisierung hilft, Ferritperlen nicht als „Bauteil aus Gewohnheit“, sondern als gezielt eingesetztes Designwerkzeug zu verstehen.


Comment