Dans l’article précédent, nous avons expliqué l’utilisation de base de la fonction « tol », mais cette fois, nous allons aller plus loin en explorant les paramètres avancés et la personnalisation de la fonction « tol ». Nous nous concentrerons en particulier sur l’ajustement de l’écart type et la manière de simuler la répartition réelle des composants.
- Définition de l’écart type basée sur la distribution réelle des composants
- Pourquoi la tolérance est-elle définie en fonction de 3σ et non de 1σ ?
- Différence entre 1σ et 3σ
- Explication concrète
- Méthode de configuration concrète pour la simulation
- Exemple de configuration de la fonction « tol »
- Signification et impact de la configuration
Définition de l’écart type basée sur la distribution réelle des composants
Dans l’analyse de Monte Carlo, il est essentiel de reproduire avec précision les variations des composants. Comme mentionné dans l’article précédent, les erreurs de fabrication des composants suivent généralement une distribution normale, mais les fabricants gèrent les variations des composants pour qu’elles restent dans une certaine plage, dans le cadre de la gestion de la qualité.
Les résistances ayant une tolérance de ±5% sont généralement contrôlées de manière à ce que cette plage corresponde à 3σ (sigma), garantissant que 99,73% des résistances produites se situent dans cette plage, ce qui minimise le taux de produits défectueux. Dans ce cas, 1σ correspond à un tiers de la tolérance.
Pourquoi la tolérance est-elle définie en fonction de 3σ et non de 1σ ?
Dans l’industrie manufacturière, le contrôle qualité des produits utilise généralement la norme des « 3σ ». 3σ fait référence à une plage de trois écarts types autour de la moyenne dans une distribution normale, couvrant 99,73% des données. C’est une méthode standard pour minimiser les produits défectueux.
Par exemple, pour une résistance de valeur nominale de 100Ω avec une tolérance de ±5% (de 95Ω à 105Ω), les fabricants veillent à ce que cette plage couvre 99,73% de l’ensemble des produits. Cela signifie que la plage de ±5% correspond à 3σ.
Différence entre 1σ et 3σ
1σ (1 sigma) couvre environ 68,27% des données dans une distribution normale autour de la moyenne. Si la tolérance était définie en fonction de 1σ, seuls 68,27% des produits se situeraient dans cette plage, ce qui représente une plus grande dispersion des données par rapport à 3σ, où 99,73% des produits se situent dans cette plage.
En utilisant la norme des 3σ, il est possible de garantir que presque tous les produits se situent dans la plage attendue, ce qui est crucial pour le contrôle de la qualité. Une plage de tolérance définie à 3σ permet de maintenir le taux de produits défectueux à un niveau très bas.
Explication concrète
Par exemple, pour une résistance de 100Ω avec une tolérance de ±5%, il est attendu que les valeurs réelles des résistances se situent entre 95Ω et 105Ω.
Définition de 3σ : Les fabricants configurent leurs processus de manière à ce que 99,73% des produits se situent dans la plage de 95Ω à 105Ω (±5%). Cela signifie que cette plage correspond à 3σ. Par conséquent, 1σ équivaut à un tiers de cette plage (≈ 1,67Ω).
Calcul de 1σ : Étant donné que la plage de ±5% correspond à 3σ, 1σ représente un tiers de cette plage. Par conséquent, pour une résistance de 100Ω, 1σ est d’environ 1,67Ω (5Ω ÷ 3 ≈ 1,67Ω).
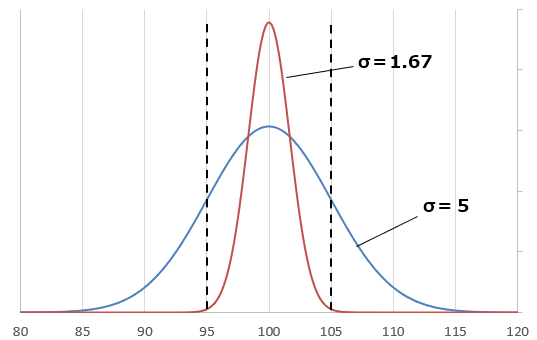
Ainsi, si le processus de fabrication est géré selon la norme des 3σ, la plage de tolérance (±5%) couvre 99,73% des produits. Cette configuration garantit la fiabilité et la qualité des produits tout en maintenant le taux de produits défectueux à moins de 0,27%.
Méthode de configuration concrète pour la simulation
Examinons l’exemple d’une résistance de 100Ω avec une tolérance de ±5%. Si nous supposons que cette plage correspond à 3σ, l’écart type 1σ se calcule de la manière suivante :
σ = (100 × 0.05) / 3 ≈ 1,67 Ω
En utilisant cette valeur de 1σ pour configurer la fonction « tol », vous pouvez simuler plus précisément la répartition réelle des composants.
Exemple de configuration de la fonction « tol »
Pour simuler cette déviation standard dans QucsStudio, utilisez la configuration suivante de la fonction « tol » :
tol(100, 1.67, 0)
Ici, 100 représente la valeur nominale de la résistance, 1,67 correspond à l’écart type (tolérance), et 0 indique une distribution normale. Avec cette configuration, les résultats de l’analyse de Monte Carlo refléteront les variations des composants basées sur le processus de fabrication réel.
Signification et impact de la configuration
En configurant avec précision l’écart type, les résultats de la simulation se situeront dans la plage de 95Ω à 105Ω avec une probabilité de 99,73%, correspondant à la distribution réelle des composants. Cela permet aux concepteurs d’évaluer plus précisément les performances des circuits dans un environnement de fabrication réel.
Prendre en compte les variations réelles des composants dans la simulation améliore non seulement la fiabilité de la conception, mais contribue également à la gestion de la qualité des produits.
コメント