No artigo anterior, explicamos o uso básico da função “tol”, mas desta vez vamos nos aprofundar nas configurações avançadas e na personalização da função “tol”. Vamos nos concentrar especialmente no ajuste do desvio padrão e na forma de simular a distribuição real dos componentes.
Configuração do Desvio Padrão com Base na Distribuição Real dos Componentes
Na análise de Monte Carlo, é importante reproduzir com precisão a variação dos componentes. Como mencionado no artigo anterior, os erros de fabricação dos componentes geralmente seguem uma distribuição normal, mas os fabricantes garantem que a variação dos componentes fique dentro de um intervalo específico como parte do controle de qualidade.
Os resistores especificados com uma tolerância de ±5% são controlados de forma que este intervalo corresponda a 3σ (sigma), garantindo que 99,73% dos resistores produzidos fiquem dentro desse intervalo, minimizando assim a taxa de produtos defeituosos. Neste caso, 1σ corresponde a um terço da tolerância especificada.
Por que a Tolerância é Definida em 3σ e Não em 1σ?
Na indústria de manufatura, o controle de qualidade dos produtos geralmente utiliza o padrão de “3σ”. 3σ refere-se a um intervalo de três desvios padrão em torno da média em uma distribuição normal, cobrindo 99,73% dos dados. Esta é uma maneira padrão de minimizar produtos defeituosos.
Por exemplo, para um resistor com um valor nominal de 100Ω e uma tolerância de ±5% (de 95Ω a 105Ω), os fabricantes garantem que este intervalo cubra 99,73% de todos os produtos. Isso significa que o intervalo de ±5% corresponde a 3σ.
Diferença entre 1σ e 3σ
1σ (1 sigma) cobre aproximadamente 68,27% dos dados em uma distribuição normal em torno da média. Se a tolerância fosse definida com base em 1σ, apenas 68,27% dos produtos ficariam dentro deste intervalo, indicando uma maior dispersão dos dados em comparação com 3σ, onde 99,73% dos produtos estão dentro desse intervalo.
Usar o padrão de 3σ permite garantir que quase todos os produtos estejam dentro do intervalo esperado, o que é crucial para o controle de qualidade. Definir o intervalo de tolerância em 3σ permite manter uma taxa de produtos defeituosos muito baixa.
Explicação Concreta
Por exemplo, para um resistor de 100Ω com uma tolerância de ±5%, espera-se que os valores reais dos resistores fiquem entre 95Ω e 105Ω.
Definição de 3σ: Os fabricantes configuram seus processos para garantir que 99,73% dos produtos fiquem dentro do intervalo de 95Ω a 105Ω (±5%). Isso significa que esse intervalo corresponde a 3σ. Assim, 1σ equivale a um terço desse intervalo (≈ 1,67Ω).
Cálculo de 1σ: Como o intervalo de ±5% corresponde a 3σ, 1σ representa um terço deste intervalo. Portanto, para um resistor de 100Ω, 1σ é de aproximadamente 1,67Ω (5Ω ÷ 3 ≈ 1,67Ω).
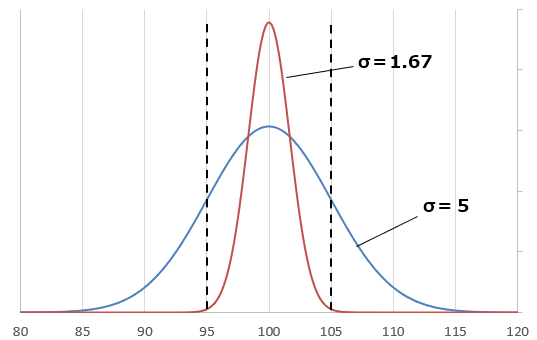
Assim, se o processo de fabricação for gerenciado de acordo com o padrão de 3σ, o intervalo de tolerância (±5%) cobrirá 99,73% dos produtos. Esta configuração garante a confiabilidade e a qualidade dos produtos, mantendo a taxa de produtos defeituosos abaixo de 0,27%.
Método de Configuração Concreta para Simulação
Vamos considerar o exemplo de um resistor de 100Ω com uma tolerância de ±5%. Se assumirmos que esse intervalo corresponde a 3σ, o desvio padrão 1σ é calculado da seguinte forma:
σ = (100 × 0.05) / 3 ≈ 1,67 Ω
Ao usar esse valor de 1σ para configurar a função “tol”, é possível simular mais precisamente a distribuição real dos componentes.
Exemplo de Configuração da Função “tol”
Para simular essa variação padrão no QucsStudio, utilize a seguinte configuração para a função “tol”:
tol(100, 1.67, 0)
Aqui, 100 representa o valor nominal do resistor, 1,67 corresponde ao desvio padrão (tolerância), e 0 indica uma distribuição normal. Com esta configuração, os resultados da análise de Monte Carlo refletirão as variações dos componentes com base no processo de fabricação real.
Significado e Impacto da Configuração
Ao configurar precisamente o desvio padrão, os resultados da simulação estarão no intervalo de 95Ω a 105Ω com uma probabilidade de 99,73%, correspondendo à distribuição real dos componentes. Isso permite que os projetistas avaliem com mais precisão o desempenho dos circuitos em um ambiente de fabricação real.
Considerar as variações reais dos componentes na simulação não só melhora a confiabilidade do projeto, mas também contribui para o controle de qualidade dos produtos.
コメント