uSimmics(旧Qucs)でトランジェント解析を行うと、信号の立ち上がり直後に、波形がギザギザと振動することがあります。この現象がリンギング(ringing)です。
初めてこの波形を見たとき、「ノイズが乗っているのでは?」「シミュレーション条件がおかしいのでは?」と感じる人は少なくありません。しかしリンギングは、偶然でも不具合でもありません。回路がそう振る舞うように決まっている、非常に基本的な物理現象です。
この記事では、uSimmicsを使ってリンギングだけを意図的に発生させる最小回路を作り、波形を見ながらその正体を整理します。
uSimmicsでリンギングを確認するときの考え方
uSimmicsでリンギングを確認するときは、余計な要因を入れず、できるだけ単純な回路にします。
- 伝送線路は使わない
- 回路は局所的にまとめる
- L と C が支配的になる構成にする
これだけ意識すると、立ち上がり直後の「ギザギザ」が、LC共振によるリンギングだと波形で素直に確認できます。
リンギングは設計者が最初に出会う物理現象
リンギングは、高速信号設計において多くの設計者が最初に出会う物理現象です。配線を少し引き回しただけで、ICを少し高速な品種に変えただけで、それまで見えていなかった振動が突然現れます。
このとき起きているのは、設計ミスでもツールの癖でもありません。それまで無視できていたL と C が、無視できなくなっただけです。
リンギングの正体は L と C の共振
リンギングの原因は、回路中に存在するインダクタンス(L)とキャパシタンス(容量C)です。特別な部品を置いていなくても、配線やビア、電流ループはLとして、ICの入力容量や寄生容量はCとして必ず存在します。
信号が立ち上がる瞬間、エネルギーが一気に回路へ注入されると、L と C の間でエネルギーのやり取りが始まります。これが共振であり、uSimmicsの波形で見える「ギザギザ」の正体です。
uSimmicsで見るリンギングの再現性
uSimmicsでリンギングを観察していると、毎回ほぼ同じ周期、同じ形で振動が出ることに気づきます。これはリンギングが「たまたま出たノイズ」ではなく、回路構成によって決まっている現象だからです。
L と C を固定したまま何度シミュレーションを回しても、結果はほとんど変わりません。この再現性こそが、リンギングが設計で扱える現象であることを示しています。
最小回路でリンギングだけを確認する
リンギングを理解するためには、反射などの要因を混ぜず、リンギングだけが支配的になる最小回路を作るのが近道です。
ここでは回路構成を固定し、抵抗 R だけを変えたときの波形を比較します。これにより、リンギングの「出方」と「収まり方」を素直に観察できます。
リンギング確認用・最小回路
VPulse ─ R ─ L ──●── Vout
|
C
|
GND
観測点は Vout(コンデンサ C の上側)です。この点では、立ち上がり直後のリンギングが最も分かりやすく現れます。
回路定数(共通条件)
以下の条件は、すべてのケースで共通です。L と C を固定し、抵抗 R だけを変更してリンギングの違いを見ます。
- VPulse:0 → 1 V、Tr = 0.1 ns、Tf = 0.1 ns
- L:10 nH(配線・ループ相当)
- C:10 pF(IC入力容量相当)
- R:1 Ω(基準)→ 5 Ω → 10 Ω(比較)
L=10nH、C=10pFの場合、リンギングの周期はおよそ2ns程度になります。
ケース1:R = 1 Ω(基準)
まずは R=1Ω の波形で、リンギングの基本的な見え方を確認します。R が小さいため減衰が弱く、リンギングがはっきりと長く続く波形になります。
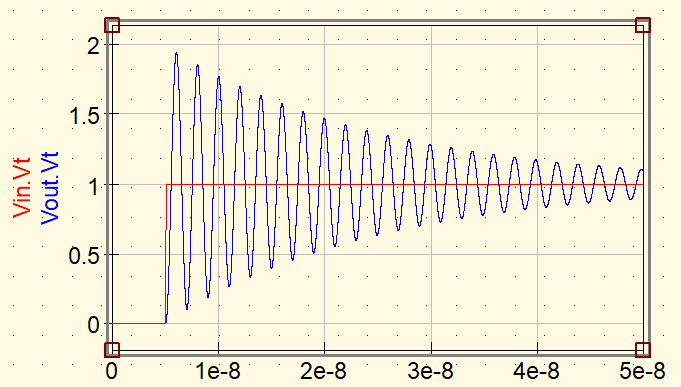
- 振幅が大きい
- 振動がなかなか収束しない
- 周期は約 2ns
ケース2:R = 5 Ω(中間)
次に R=5Ω の波形です。R を大きくすると、リンギングの振幅が小さくなり、収束が早くなります。
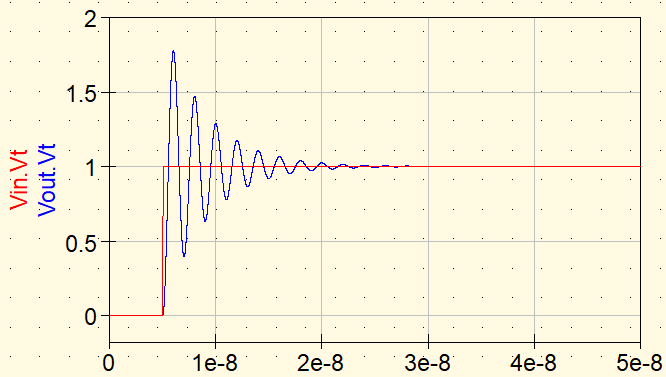
- 周期はほぼ同じ
- 振動の回数が減る
- 立ち上がり後のギザギザが目立ちにくくなる
R を変えても周期は変わらないことが、波形比較から直感的に分かります。
ケース3:R = 10 Ω(強い減衰)
最後に R=10Ω の波形です。R をさらに大きくすると、リンギングはごく短時間で収束します。条件によっては「ほとんど見えない」レベルになることもあります。
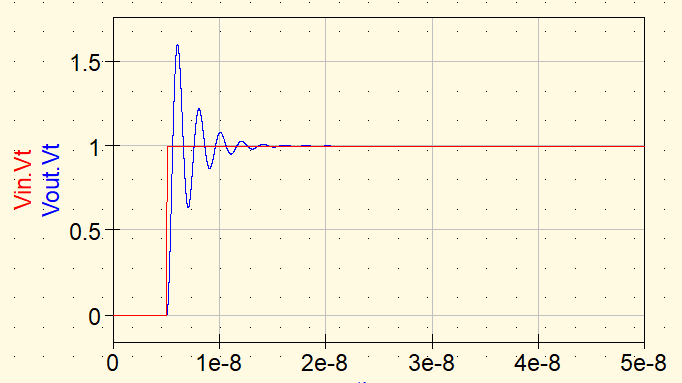
- 周期は変わらない
- 振幅が小さく、すぐに落ち着く
- 「消えた」ではなく「強く減衰して見えにくい」
3つの波形を並べて分かること
3つの波形を比べると、次の点がはっきりします。
- リンギングの周期は L と C で決まる
- 抵抗 R は、周期を変えずに減衰の強さだけを変える
- 抵抗は共振を「止める」のではなく、エネルギーを逃がして落ち着かせている
この比較ができると、「なぜ直列抵抗やダンピング抵抗が効くのか」が式を使わなくても理解できます。
最小回路は実基板の縮図
この回路は極端に単純ですが、実際の基板で起きている現象と本質は同じです。
- 配線が長くなる
- ループが大きくなる
- ICの入力容量が増える
これらはすべて、この回路の L や C が大きくなる方向に働きます。uSimmicsで作った最小回路は、実基板で起きているリンギングを観察しやすい形に切り出したものにすぎません。
まとめ:抵抗を変えるとリンギングの「収まり方」が変わる
- リンギングは L と C の共振による振動
- 立ち上がり直後に現れる
- 周期は L と C で決まる
- 抵抗 R は振動を減衰させるために効く
R を変えた波形を並べて確認すると、リンギングは「謎のノイズ」ではなく、設計で理解し、調整できる現象だと分かります。




Comment