Las perlas de ferrita se utilizan ampliamente como medida de supresión de ruido. Es común verlas en líneas de alimentación y líneas de E/S, y en muchos casos se tratan simplemente como “un componente que se coloca por si acaso”.
Sin embargo,
- No se puede explicar claramente por qué funcionó
- No se entiende por qué esta vez no funcionó
- La diferencia con un inductor no está bien definida
Si se siguen utilizando las perlas de ferrita de esta manera, las decisiones de diseño tienden a depender excesivamente de la experiencia individual.
En este artículo, organizamos la pregunta de “por qué funciona una perla de ferrita” utilizando un modelo de circuito mínimo que puede reproducirse en uSimmics (antes QucsStudio). La conclusión es clara desde el principio: una perla de ferrita funciona no porque sea un inductor.
- Conclusión del artículo
- Un error común: “perla de ferrita = inductor”
- Circuito base común para la comparación en uSimmics
- Comparación de formas de onda: cuatro casos bajo las mismas condiciones
- Conclusiones de la comparación de las cuatro formas de onda
- ¿Por qué no usar simplemente una resistencia?
- Casos típicos en los que funciona / no funciona
- La colocación lo es todo: dónde ponerla
- Resumen
Conclusión del artículo
- Una perla de ferrita no es un inductor ideal
- Su esencia no es “reflejar el ruido y detenerlo”
- Funciona al disipar la energía de alta frecuencia como pérdida (calor)
- Por eso el ringing se reduce y la señal se estabiliza
En otras palabras, desde el punto de vista EMC, una perla de ferrita es un elemento con pérdidas dependientes de la frecuencia. Con esta perspectiva, resulta mucho más sencillo explicar cuándo funciona, cuándo no, dónde colocarla y qué alternativas (R o RC) pueden utilizarse.
Un error común: “perla de ferrita = inductor”
A menudo se describe a la perla de ferrita como “alta impedancia a alta frecuencia” o “con un componente inductivo”. Esto no es incorrecto, pero si nos quedamos solo con esa explicación, surge una pregunta importante.
Si la impedancia simplemente aumenta, ¿por qué se reduce el ringing?
Si el aumento de impedancia fuera la única razón, una reflexión más fuerte haría que el ringing se intensificara (aumentando el factor Q). Para aclararlo, primero verificamos el caso de insertar un inductor ideal en uSimmics.
Circuito base común para la comparación en uSimmics
Usamos el siguiente circuito mínimo como base común y comparamos cuatro casos cambiando únicamente el elemento en serie. El punto de observación es Vout (nodo superior de Cload).
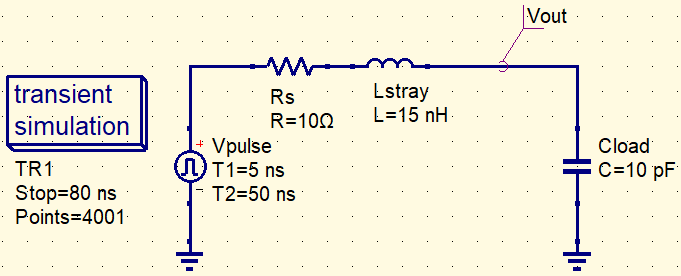
Parámetros recomendados (ejemplo)
Los siguientes valores son solo un ejemplo para facilitar la comparación del ringing y del efecto de la perla de ferrita en uSimmics. Ajuste el tiempo de subida y los valores de los componentes según su circuito real.
| Elemento | Valor | Propósito |
|---|---|---|
| VPulse | 0 → 1 V | Observar claramente la respuesta al escalón |
| Tr / Tf | 1 ns | Tiempo de subida/bajada para comparación clara |
| Ancho de pulso | 50 ns | Observar suficientemente el comportamiento posterior |
| Rs | 10 Ω | Modelo de resistencia de salida del driver |
| Lstray | 15 nH | Inductancia parásita (traza/encapsulado) |
| Cload | 10 pF | Carga + capacitancia parásita |
Configuración Transient (ejemplo)
- Stop time: 80 ns
- Max step: 20 ps (reducir si el ringing no se resuelve)
Nota: estos valores se utilizan con fines educativos y de visualización. En una placa real, sustituya L/C/R por valores acordes a su diseño.
Comparación de formas de onda: cuatro casos bajo las mismas condiciones
A continuación se insertan cuatro gráficos de forma de onda. Asegúrese de guardar los cuatro con la misma escala en los ejes X/Y para que la comparación sea clara.
Forma de onda ①: Sin contramedidas
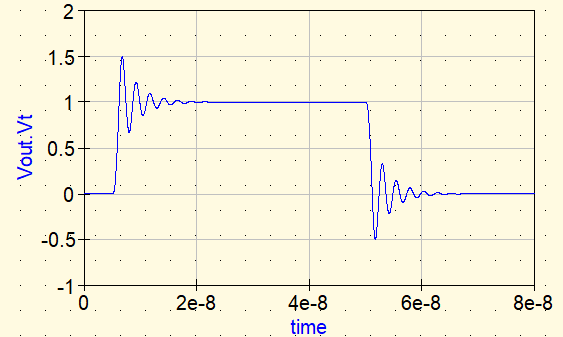
Sin contramedidas, Vout presenta un sobreimpulso tras el flanco de subida y luego continúa oscilando. Esto se debe a la resonancia formada por Lstray y Cload. Cuanto menor es la pérdida, más tiempo persiste la oscilación.
Forma de onda ②: Inductor ideal
A continuación, insertamos un inductor ideal como elemento en serie.
- Lideal: 100 nH (ejemplo)
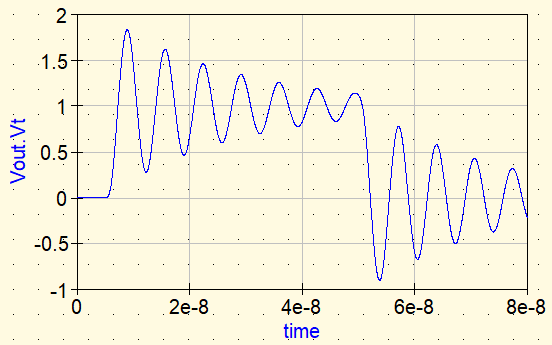
Aunque suene razonable pensar que “una mayor impedancia a alta frecuencia debería detener el ruido”, un inductor ideal no tiene pérdidas. La energía resonante permanece en el circuito y el ringing no se atenúa rápidamente.
Punto clave: no es la impedancia alta lo que detiene el ringing, sino la presencia de pérdidas.
Forma de onda ③: Resistencia ideal
Luego insertamos una resistencia ideal en serie.
- Rideal: 10 Ω (ejemplo)
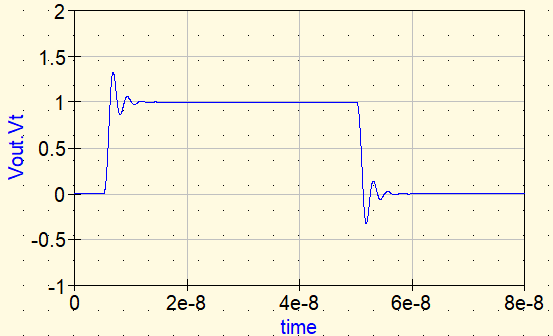
Con la resistencia, el ringing se atenúa visiblemente. La razón es simple: la energía de la oscilación se disipa como calor en la resistencia.
En otras palabras, lo que realmente detiene el ringing no es la impedancia, sino la pérdida (R).
Forma de onda ④: Perla de ferrita
Finalmente, realizamos una simulación usando una perla de ferrita real. Aquí la insertamos como un componente de parámetros S (2 puertos) en serie.
- Perla de ferrita utilizada: BLM03AG601SN1 (Murata)
- Parámetros S (.s2p): disponibles en el sitio web de Murata
Dado que la perla de ferrita tiene un comportamiento dependiente de la frecuencia, el uso de parámetros S permite observar una respuesta más realista en el dominio temporal.
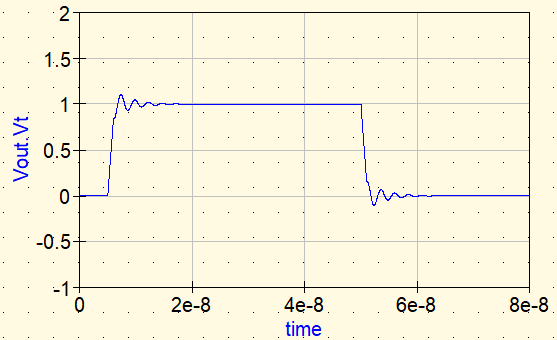
Al insertar la perla de ferrita mediante parámetros S, el ringing se reduce de forma similar al caso de la resistencia ideal. La diferencia clave es su dependencia con la frecuencia.
Mientras que una resistencia introduce pérdidas desde DC, la perla de ferrita incrementa la pérdida principalmente en la banda de alta frecuencia deseada. Así, disipa la energía de los componentes de alta frecuencia del flanco, minimizando el impacto en DC y baja frecuencia.
Conclusiones de la comparación de las cuatro formas de onda
- Sin contramedidas: la resonancia aparece directamente
- Inductor ideal: difícil de amortiguar (sin pérdidas)
- Resistencia ideal: se amortigua (con pérdidas)
- Perla de ferrita: se amortigua (pérdidas a alta frecuencia)
Por lo tanto, una perla de ferrita funciona no porque sea un inductor, sino porque introduce pérdidas, y además puede hacerlo de forma selectiva en frecuencia.
¿Por qué no usar simplemente una resistencia?
Es natural preguntarse: “¿por qué no basta con añadir una resistencia?”. En efecto, una resistencia puede suprimir el ringing.
Sin embargo, una resistencia tiene desventajas:
- Caída de tensión incluso en DC
- Mayor disipación de potencia
- Mayor impacto en la señal o la calidad de la alimentación
En cambio, la perla de ferrita tiene poco impacto en DC y baja frecuencia, y actúa como pérdida donde realmente se necesita. Por eso puede considerarse como una “resistencia que solo actúa donde hace falta”.
Casos típicos en los que funciona / no funciona
Casos en los que suele funcionar
- Ringing de alta frecuencia en líneas de alimentación
- Ruido causado por flancos rápidos de señales digitales
- Cuando las emisiones radiadas están dominadas por componentes de alta frecuencia
Casos en los que no funciona o puede empeorar
- El ruido dominante es de baja frecuencia y no coincide con la banda de pérdidas
- Se crea una nueva resonancia después de la perla
- La ruta de retorno (GND) es larga y la energía no se disipa como se espera
La colocación lo es todo: dónde ponerla
Una perla de ferrita no es una “pared”. Más bien, es una salida para desechar energía.
Por ello, su efecto es máximo cuando se coloca:
- Cerca de la fuente de ruido
- Justo antes de que la energía de alta frecuencia se propague
- En un punto con una ruta de retorno (GND) corta y clara
Colocarla teniendo en cuenta estos puntos maximiza el efecto.
Resumen
Una perla de ferrita funciona no porque sea un inductor, sino porque disipa la energía de alta frecuencia como pérdida. Por eso un inductor ideal no detiene el ringing, mientras que una resistencia o una perla de ferrita (elementos con pérdidas) permiten que la forma de onda se estabilice más rápido.
Al mismo tiempo, una perla de ferrita no funciona en todas las situaciones. Si la característica de pérdidas no coincide con la frecuencia del ringing, la forma de onda puede ser casi idéntica al caso “sin contramedidas”. La colocación y la ruta de retorno también influyen en cómo se disipa la energía.
Al comparar circuitos en uSimmics, se puede ver claramente en las formas de onda que no es simplemente la “alta impedancia” lo que ayuda, sino dónde y en qué frecuencia se amortigua la energía. Esta visualización permite entender la perla de ferrita no como un componente “por costumbre”, sino como una herramienta de diseño utilizada con criterio.
Comment