QucsStudio中的蒙特卡洛模拟参数设置方法

在利用QucsStudio的仿真功能时，蒙特卡洛分析是一种特别强大的工具。在上一篇文章中，我们介绍了低通滤波器设计的基础知识，这次我们将重点介绍蒙特卡洛分析中的tol函数，详细说明其使用方法和适用范围。

之所以关注tol函数，是因为在进行蒙特卡洛分析时，许多用户不知道如何设置元件的波动，或者由于对参数缺乏理解而进行错误的仿真。在现实的电路设计中，像电阻和电容这样的元件会因制造误差和环境因素而产生波动。正确地建模这些波动，对于提高仿真精度至关重要。

然而，许多用户不熟悉tol函数的参数设置，无法正确指定波动的范围和分布类型。结果是，仿真结果往往不能反映实际操作，导致错误的结论。

通过正确设置tol函数，您可以更准确地评估电路性能，并模拟制造误差和环境变化的影响。这使得在设计阶段的考虑更加贴近现实，并在确保电路的可靠性和性能方面提供了极大的帮助。

什么是蒙特卡洛仿真？

蒙特卡洛仿真是一种理解伴随不确定性的系统或过程的方法。此仿真通过使用各种随机值作为系统的输入，反复进行计算。通过分析结果分布，您可以了解系统在多大程度上出现特定结果，并评估系统的性能和可靠性。

例如，如果电阻器或电容器等元件由于制造过程具有±5％的波动，蒙特卡洛分析的目的是模拟这些波动如何影响整个电路。

要进行蒙特卡洛仿真，您需要设置用于仿真的输入变量的波动。在QucsStudio中，有一个名为tol的函数，可以轻松设置这些波动。

通过使用tol函数，您可以轻松指定数据的波动范围。例如，通过定义特定电阻值围绕其平均值的波动程度，您可以在仿真中反映实际制造误差和操作环境的波动。此函数用于在蒙特卡洛仿真中模拟变量的随机波动。

QucsStudio中的tol函数使用三个参数 x, v, d 来指定变量的波动，并模拟随机波动。

tol(x, v, d)

例如，考虑一个偏差为100Ω±10％的电阻器，可以使用tol函数表示如下。平均值是波动的中心值，在这种情况下为“100”。容许范围表示波动的范围，因此对于±10％，设置为“10”。

tol函数的分布类型有两种，每种都有不同的特性。分布类型非常重要，如果理解不正确，仿真可能不会在预期范围内进行。正态分布和均匀分布的区别如下：

以平均值100、容许范围10％为例，每种分布的图如下所示：

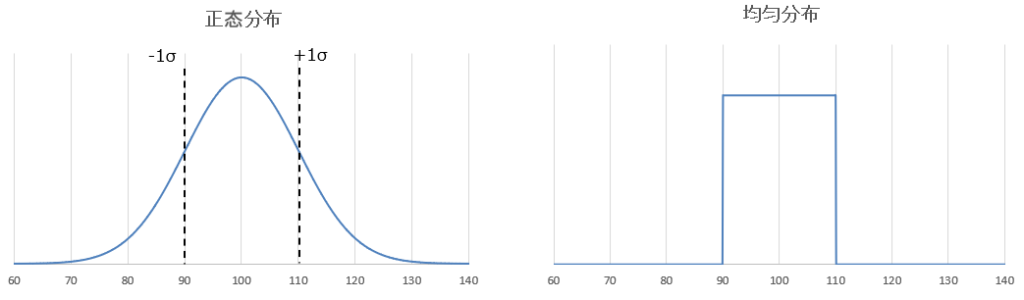
首先，对于正态分布，如图所示，它变为以100为中心的高斯分布。将容许范围（v）设置为±10％会产生标准偏差（σ）为10Ω的正态分布数据分布。需要注意的是，在90~110Ω范围之外也会发生分布，这意味着波动范围不完全是±10％。

对于均匀分布，它非常简单，范围为±10％，即数据均匀分布在90到110Ω之间，超出此范围没有数据。这意味着波动的上限和下限在10％范围内。然而，由于数据范围的中心与上下限的比例相等，因此不适合验证实际元件的波动比例。实际的电子元件在范围的中心附近分布最多，波动越接近上下限越少，形成正态分布。

实际上，电阻和电容等元件的波动是正态分布而不是均匀分布。如前所述，直接使用元件的偏差（％）作为容许范围（v）无法进行准确的仿真。模拟实际元件分布的方法将在另一篇文章中介绍。

通过使用tol函数，您可以在蒙特卡洛仿真中有效地模拟输入变量的随机波动。理解并正确设置正态分布和均匀分布的特性，可以高精度地评估系统的性能和可靠性。