Die Monte-Carlo-Analyse ist ein besonders leistungsfähiges Werkzeug, wenn es um die Nutzung der Simulationsfunktionen von QucsStudio geht. Im letzten Artikel haben wir die Grundlagen der Tiefpassfilter-Entwicklung besprochen. Diesmal konzentrieren wir uns auf die tol-Funktion, um ihre Anwendung und ihren Geltungsbereich im Detail zu erläutern.
Der Grund für den Fokus auf die tol-Funktion liegt darin, dass viele Benutzer bei der Durchführung einer Monte-Carlo-Analyse unsicher sind, wie sie die Variabilität der Bauteile einstellen sollen. Dies führt oft zu falschen Simulationen aufgrund unzureichenden Verständnisses der Parameter. In der realen Schaltungsentwicklung führen Fertigungstoleranzen und Umwelteinflüsse zu Schwankungen bei Bauteilen wie Widerständen und Kondensatoren. Eine korrekte Modellierung dieser Schwankungen ist entscheidend für die Genauigkeit der Simulation.
Viele Benutzer sind jedoch mit der Parametereinstellung der tol-Funktion nicht vertraut und können die Schwankungsbereiche und Verteilungen nicht korrekt spezifizieren. Dies führt dazu, dass die Simulationsergebnisse die tatsächlichen Bedingungen nicht widerspiegeln, was zu falschen Schlussfolgerungen führen kann.
Durch die korrekte Einstellung der tol-Funktion kann die Schaltungsleistung genauer bewertet und die Auswirkungen von Fertigungstoleranzen und Umwelteinflüssen simuliert werden. Dies ermöglicht es, die Überlegungen in der Entwurfsphase realistischer zu gestalten und die Zuverlässigkeit und Leistung der Schaltung zu sichern.
Was ist eine Monte-Carlo-Simulation?
Die Monte-Carlo-Simulation ist eine Methode zur Analyse von Systemen oder Prozessen, die mit Unsicherheiten behaftet sind. Bei dieser Simulation werden für die Eingaben des Systems zufällige Werte verwendet, und die Berechnung wird mehrfach wiederholt. Die Ergebnisse werden gesammelt, um die Verteilung zu analysieren. Durch die Analyse dieser Verteilung kann man herausfinden, wie häufig das System bestimmte Ergebnisse liefert und die Leistung oder Zuverlässigkeit des Systems bewerten.
Zum Beispiel, wenn Widerstände oder Kondensatoren während des Herstellungsprozesses eine Toleranz von ±5 % aufweisen, simuliert die Monte-Carlo-Analyse, wie sich diese Toleranz auf das Gesamtsystem auswirkt.
Modellierung des Schwankungsbereichs
Um eine Monte-Carlo-Simulation durchzuführen, muss die Variabilität der Eingabevariablen eingestellt werden. In QucsStudio gibt es die tol-Funktion, die die Festlegung dieser Variabilität erleichtert.
Mit der tol-Funktion kann der Schwankungsbereich der Daten einfach spezifiziert werden. Zum Beispiel kann definiert werden, wie stark ein bestimmter Widerstandswert um den Mittelwert schwankt, um die tatsächlichen Fertigungstoleranzen oder Umwelteinflüsse in der Simulation zu berücksichtigen. Diese Funktion dient zur Simulation der zufälligen Variabilität der Variablen in einer Monte-Carlo-Simulation.
Syntax der tol-Funktion
Die tol-Funktion in QucsStudio verwendet drei Argumente, x, v und d, um die Variabilität einer Variablen zu spezifizieren und zufällige Schwankungen zu simulieren.
tol(x, v, d)- x: Mittelwert
- v: Toleranzbereich (%)
- d: Verteilungstyp (0 = Normalverteilung, 1 = Gleichverteilung, Standard ist 0)
Als Beispiel betrachten wir einen Widerstand mit einem Nennwert von 100 Ω und einer Toleranz von ±10 %. In der tol-Funktion wird dies wie folgt angegeben: Der Mittelwert wird auf „100“ gesetzt, da dies der zentrale Wert der Schwankung ist. Der Toleranzbereich wird auf „10“ gesetzt, da die Schwankung ±10 % beträgt.
Was ist der Verteilungstyp?
Die tol-Funktion unterstützt zwei Verteilungstypen, die jeweils unterschiedliche Eigenschaften aufweisen. Das Verständnis dieser Verteilungstypen ist entscheidend, um sicherzustellen, dass die Simulation innerhalb des vorgesehenen Bereichs durchgeführt wird. Der Unterschied zwischen Normalverteilung und Gleichverteilung ist:
- Normalverteilung: Die Daten sind symmetrisch um den Mittelwert verteilt, wobei die Wahrscheinlichkeit für Werte, die weiter vom Mittelwert entfernt sind, geringer ist. Die Verteilung hat die Form einer Glockenkurve.
- Gleichverteilung: Die Daten sind gleichmäßig über den angegebenen Bereich verteilt, wobei jeder Wert innerhalb des Bereichs die gleiche Wahrscheinlichkeit hat. Die Verteilung hat die Form eines Rechtecks.
Die Diagramme für beide Verteilungen bei einem Mittelwert von 100 und einem Toleranzbereich von ±10 % sehen wie folgt aus:
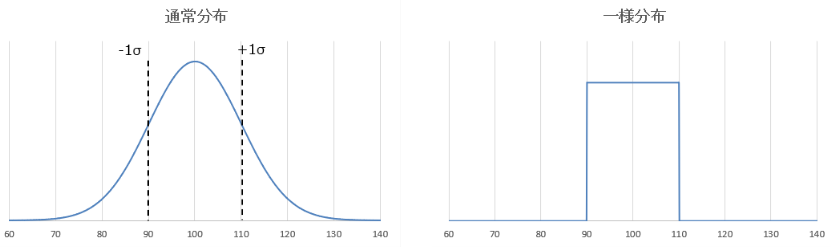
Die Normalverteilung zeigt eine symmetrische Verteilung um 100, wobei die Standardabweichung (σ) bei einer Toleranz von ±10 % 10 Ω beträgt. Es ist wichtig zu beachten, dass auch Werte außerhalb des Bereichs von 90 bis 110 Ω auftreten können, da die Schwankungen nicht strikt auf ±10 % begrenzt sind.
Bei der Gleichverteilung hingegen ist die Datenverteilung gleichmäßig über den Bereich von 90 bis 110 Ω verteilt, und es gibt keine Werte außerhalb dieses Bereichs. Dies bedeutet, dass die Schwankungen strikt innerhalb der ±10 % liegen. Da jedoch alle Werte im Bereich gleich wahrscheinlich sind, ist diese Verteilung weniger geeignet, um die tatsächlichen Fertigungstoleranzen elektronischer Bauteile zu simulieren, die typischerweise einer Normalverteilung folgen.
Hinweise zur Einstellung
Die tatsächlichen Schwankungen von Widerständen und Kondensatoren folgen in der Regel einer Normalverteilung. Wie zuvor beschrieben, führt die Verwendung des Bauteilfehlers in Prozent als Toleranzwert in der tol-Funktion zu ungenauen Simulationen. In einem separaten Artikel werden wir erläutern, wie die tatsächlichen Bauteilabweichungen korrekt simuliert werden können.
Fazit
Mit der tol-Funktion können in Monte-Carlo-Simulationen die zufälligen Schwankungen der Eingabevariablen effektiv simuliert werden. Durch das Verständnis der Eigenschaften von Normal- und Gleichverteilung und deren korrekte Einstellung kann die Leistung und Zuverlässigkeit des Systems präzise bewertet werden.
コメント