在上一篇文章中，我们解释了 “tol” 函数的基本使用方法。这次，我们将深入探讨 “tol” 函数的详细设置和自定义。特别是，我们将详细介绍标准差的调整，以及如何模拟实际组件的分布。
基于实际组件分布的标准差设置
在蒙特卡罗分析中，准确再现组件的波动非常重要。正如我们在上一篇文章中提到的，组件的制造误差通常遵循正态分布。制造商通过质量控制确保这些波动在特定范围内。
通常，具有±5%容差的电阻器在制造过程中管理为符合3σ（3西格玛）标准。这样可以确保制造的电阻器中有99.73%落在±5%的范围内，从而降低了不合格产品的出现率。在这种情况下，1σ相当于容差范围的1/3。
为什么容差是3σ而不是1σ？
在制造业中，通常使用”3σ (3西格玛)” 标准进行质量控制。这里，3σ指的是正态分布的均值加减三个标准差（σ）的范围内，99.73%的数据都在该范围内。这种方法用于将不合格产品最小化。
例如，对于一个标称值为100Ω、容差为±5%（95Ω到105Ω）的电阻器，制造商确保99.73%的产品落在此范围内。这意味着±5%的范围对应于3σ。
1σ和3σ的区别
1σ（1西格玛）是指距均值1个标准差的范围，约68.27%的数据落在该范围内。如果容差设置为1σ，产品特性落在±1σ范围内的概率仅为68.27%。相比之下，3σ的范围更集中，覆盖了99.73%的数据。
使用3σ标准可以确保大多数产品都在预期范围内，这对质量控制至关重要。使用3σ容差可以将不合格产品的比例保持在非常低的水平。
具体说明
让我们以100Ω电阻器为例。设定容差为±5%，电阻器的实际值应落在95Ω到105Ω之间。
3σ设置: 制造商将工艺设定为使产品以99.73%的概率落在95Ω到105Ω（±5%）范围内。这意味着±5%的范围相当于3σ。因此，1σ是此范围的三分之一，即1.67Ω。
1σ计算: 由于±5%的范围对应于3σ，1σ为该范围的三分之一。对于一个100Ω的电阻器，1σ约为1.67Ω（5Ω ÷ 3 ≈ 1.67Ω）。
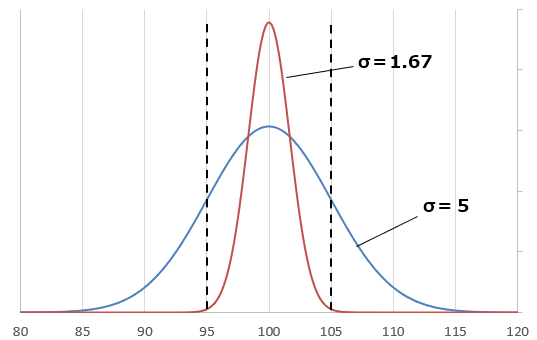
因此，当制造过程以3σ标准进行管理时，容差范围（±5%）涵盖了99.73%的产品。该设置确保了产品的可靠性和质量，将不合格率控制在0.27%以下。
具体的仿真设置方法
让我们继续以100Ω电阻器为例。如果制造误差为±5%，电阻值应落在95Ω到105Ω之间。假设该范围代表3σ，则1σ的标准差计算如下：
σ = (100 × 0.05) / 3 ≈ 1.67 Ω
通过使用此1σ值，可以设置 “tol” 函数以更准确地模拟实际的组件分布。
“tol” 函数的设置示例
在QucsStudio中，为了在仿真中反映此标准差，可以按如下方式设置 “tol” 函数：
tol(100, 1.67, 0)
这里，100 是目标电阻值（平均值），1.67 是标准差（容差），0 表示正态分布。此设置允许通过蒙特卡罗分析模拟基于实际制造过程的组件波动。
设置的意义和效果
通过准确设置标准差，仿真结果将显示99.73%的电阻值在95Ω到105Ω范围内。这与制造过程中的实际组件分布非常吻合。因此，设计人员可以更准确地评估实际制造环境中的电路性能。
考虑组件波动的仿真不仅提高了设计的可靠性，还对生产中的质量控制做出了贡献。
コメント