QucsStudio is an invaluable tool in the world of electronic circuit design and simulation. It proves particularly useful in calculating the characteristic impedance of transmission lines like striplines. While we’ve previously introduced how to calculate the characteristic impedance of a stripline using QucsStudio, this article delves deeper into the challenges faced when performing calculations on actual boards. Through this article, we aim to bridge the gap between theory and practice, providing you with more practical knowledge.
What is a Stripline?
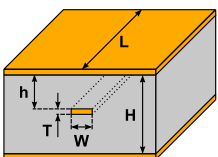
A stripline is a transmission line composed of parallel conductors embedded inside the substrate. This structure, which sandwiches the signal line between the top and bottom ground planes, suppresses electromagnetic radiation and controls signal propagation. It’s primarily used in microwave and RF (Radio Frequency) applications, being well-suited for high-frequency signal transmission.
The characteristic impedance of a stripline depends on physical parameters like the width of the signal line, the thickness of the substrate, and the dielectric constant. This impedance is crucial for impedance matching between the signal source and load; improper matching can lead to reflections and losses, degrading signal quality.
Calculating Characteristic Impedance
Using QucsStudio’s Transmission Line Calculator, you can instantly compute the characteristic impedance with just a fingertip. While this tool facilitates theoretical calculations, applying it to actual printed circuit boards brings forth new challenges. It’s essential to understand how to apply these calculations in practice, given the gap between ideal and real-world scenarios.
Issues with Etching Undercut
In the manufacturing of printed circuit boards, the subtractive method is widely used due to its efficiency and cost-effectiveness. However, this process is accompanied by a challenge known as etching undercut.
In this method, unwanted copper is chemically removed from the coated board, leaving the necessary circuit pattern on the substrate.
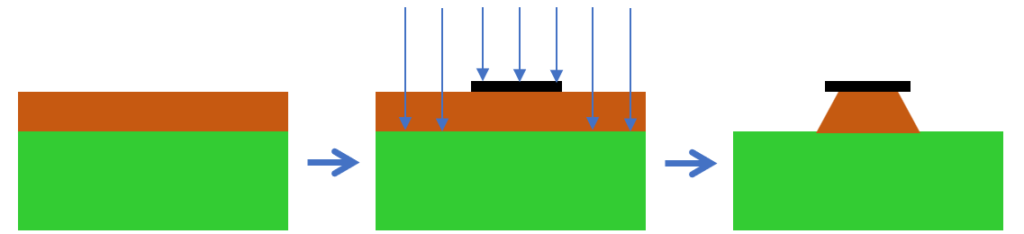
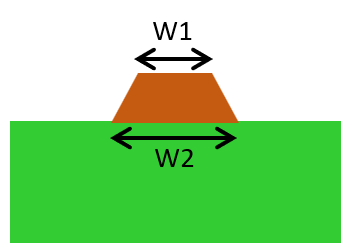
Etching undercut refers to the phenomenon where the copper layer’s sides are unintentionally dissolved at an angle during the etching process. As a result, the pattern becomes trapezoidal, tending to narrow at the top. This shape change directly impacts the characteristic impedance of striplines, especially when used for high-frequency signal transmission.
The impact of trapezoidal patterns on characteristic impedance cannot be ignored. Normally, calculations assume a constant pattern width, but if the top narrows due to etching undercut, the actual impedance tends to be higher than calculated. This discrepancy can cause signal reflections and losses, leading to reduced signal quality.
Therefore, understanding and accounting for the effects of etching undercut in impedance calculations is crucial for accurate circuit design.
The Necessity of Calculating Impedance Considering Trapezoidal Patterns
Calculating impedance while considering the impact of trapezoidal patterns is essential for accurate circuit design. In circuits dealing with high frequencies, even minor impedance mismatches can be problematic, necessitating impedance calculations with trapezoidal correction.
Properly conducting this process ensures improved signal quality and efficient circuit design.
Trapezoidal Correction Calculation
To correct for trapezoidal pattern effects, calculate the average of the top and bottom widths as follows:
W = (W1 + W2) / 2
Use this corrected width to recalculate the characteristic impedance in QucsStudio.
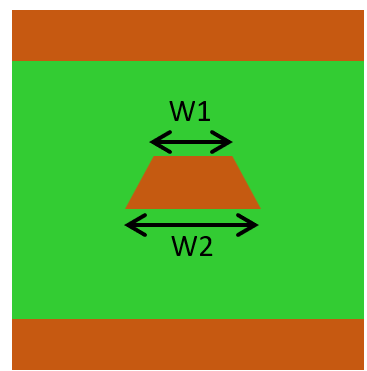
Obtain detailed finish dimensions from your board supplier.
As a rule of thumb, calculating the pattern width about 10% smaller than the specified dimensions often aligns the calculated impedance with measured values. For instance, if a pattern is designed and manufactured at 100μm width, the actual widths might be W1=80μm and W2=100μm. Therefore, calculating the characteristic impedance using a width of 90μm is advisable. This approach helps align theoretical and measured values more closely.
Conclusion
By leveraging QucsStudio, you can accurately calculate the characteristic impedance of striplines. It’s crucial to understand and correct for the effects of the subtractive method’s trapezoidal patterns. This ensures quality signal transmission and enables efficient circuit design.
📌 See the recommended reading order (Roadmap)
➡️ Next: Foot pattern impact (U.FL example)

Comment